6.2.2直线上向量的坐标及其运算
教学目标:
1.掌握直线上向量的坐标的概念;
2.会用两种方法求解直线上向量的坐标;
3.会进行直线上向量的坐标运算,会求两点间距离,会求线段的中点坐标.
教学重点:
直线上向量的坐标及其运算.
教学难点:
直线上坐标运算的灵活运用.
教学过程:
一、提出问题,解决问题:
问题1:直线上的向量能否用数来表示呢?
(1)给出直线上向量的坐标的定义:
给定一条直线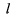 及这条直线上一个单位向量
及这条直线上一个单位向量 ,对于这条直线上的任意一个向量
,对于这条直线上的任意一个向量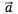 ,一定存在唯一的实数,使得
,一定存在唯一的实数,使得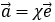 此时称为向量
此时称为向量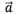 的坐标.
的坐标.
(2)让学生思考:向量 的坐标
的坐标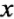 能刻画它的模与方向吗?
能刻画它的模与方向吗?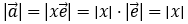 答:能.(1)
答:能.(1)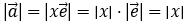
当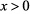 时,
时,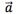 的方向与
的方向与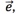 的方向相同;当
的方向相同;当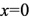 时,
时,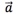 是零向量;当
是零向量;当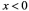 时,
时,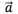 的方向与
的方向与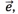 的方向相反.
的方向相反.
总结:直线上的向量完全被其坐标确定
(3)给出直线上的向量的坐标的直观理解
在直线上指定原点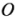 ,以
,以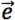 的方向为正方向,
的方向为正方向,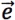 的模为单位长度建立数轴,如果把向量
的模为单位长度建立数轴,如果把向量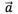 的始点平移到原点
的始点平移到原点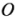 ,那么
,那么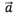 的终点对应的数就是向量
的终点对应的数就是向量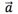 的坐标.
的坐标.
问题2:直线上的向量有了坐标之后,向量的相等以及运算与它们对应的坐标之间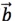 有什么关系?
有什么关系?
直线上向量的运算与坐标的关系:如果直线上两个向量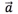 ,
,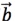 的坐标分别为
的坐标分别为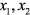

二、素养小测
思维辨析(对的打“ ”,错的打“×”)
”,错的打“×”)
(1)数轴上点A对应的数为-3,则向量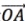 的坐标为3.()
的坐标为3.()
(2)数轴上点A对应的数为-3,则向量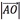 =3()
=3()
(3)直线上两个向量相等的充要条件是它们的坐标相等.()
(4)两个向量差的坐标等于这两个向量坐标的差.()
提示:(1)×.数轴上点A对应的数为-3,则向量(OA)?的坐标为-3.
(2)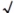 .(3)
.(3)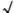 .(4)
.(4)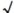 .
.
设计意图:巩固新学知识,加深理解。
三、例题讲解,深化理解
例1.如图所示,求出直线上向量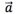 ,
,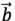 的坐标.
的坐标.
解:因为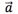 的始点在原点
的始点在原点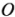 ,因此由
,因此由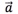 的终点坐标可知
的终点坐标可知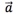 的坐标为2
的坐标为2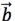 =-3
=-3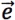
因为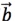 =-3所以
=-3所以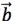 的坐标为-3
的坐标为-3
设计意图:应用两种方法求直线上的向量的坐标.

例2已知直线上向量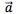 的坐标为-2,
的坐标为-2,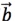 的坐标为5,求下列向量的坐标:
的坐标为5,求下列向量的坐标:
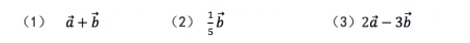

设计意图:直线上向量的坐标运算的应用.
例3.设数轴上两点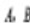 的坐标分别为3,-7,
的坐标分别为3,-7,
(1)求向量的坐标,及A,B两点间的距离.
(2)线段的中点的坐标.

设计意图:两点间距离公式及中点坐标公式的应用.
四、课堂练习,巩固所学
一、选择题

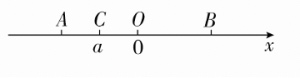
二.填空题

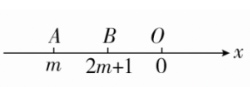
答案:1.B2.D3.A4.B5.46.3或-3 7.
五、归纳总结:
1.直线上向量的坐标的定义.
2.直线上向量坐标的两种求法.
3.直线上向量的坐标运算.
4.直线上两点间的距离公式和中点坐标公式.
本网站旨在促进我国基础教育的信息交流,促进基础教育事业的发展。本网站转载的资料,如果作者不希望我们在网上使用其作品,请立即与我们联系,我们会在收到您的意见后立即从网上移除有关内容。未经人教网的明确书面许可,任何人不得复制或对人教网所属的服务器做镜像。

