教学课时：2课时

　　教学目标：

　　1、理解平面向量的坐标的概念，会写出给定向量的坐标，会作出已知坐标表示的向量；

　　2、掌握平面向量的坐标运算，能准确表述向量的加法、减法、实数与向量的积的坐标运算法则，并能进行相关运算，进一步培养学生的运算能力；

　　3、会根据平面向量的坐标，判断向量是否共线；

　　4、通过学习向量的坐标表示，使学生进一步了解数形结合思想，认识事物之间的相互联系，培养学生辩证思维能力.

　　教学重点：

　　理解平面向量的坐标表示，平面向量的坐标运算，向量平行的充要条件的坐标表示．

　　教学难点：

　　对平面向量坐标表示的理解．

　　教学过程：

　　一、提出问题，解决问题：

　　问题1：分别与轴、轴方向相同的两单位向量能否作为基底？

　　【学生活动1】

　　学生阅读课本第160页，理解垂直、正交基底、正交分解的相关概念；

　　问题2：根据平面向量基本定理，任一向量都能用两个互相垂直的单位向量表示吗？如何表示？

　　【学生活动2】

　　学生自主讨论，并完成课本第161页上面的“尝试与发现”.

　　问题3：我们知道在直角坐标系内，平面内的每一个点都可以用一对有序实数来表示，且点与坐标是一一对应的.既然向量的起点和终点的坐标是确定的，那么向量也可以用一对实数来表示吗？向量平移后坐标发生变化吗？

　　【学生活动3】

　　学生自主讨论，并完成课本第161页图6-2-11的填空.

　　问题4：平面上的向量有了坐标之后，向量的相等以及运算与它们对应的坐标之间有什么关系？已知你能用坐标来表示吗？已知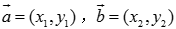，你能用坐标来表示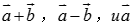吗?

　　【学生活动4】

　　学生动手证明，并完成课本第162页例2上面的填空.

　　问题5：你能由平面上的向量的坐标得到向量的模吗？

　　【学生活动5】

　　学生小组讨论，尝试各种方法，得到结论.

　　问题6：已知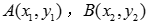，怎么用坐标表示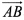和AB的中点坐标呢？

　　【学生活动6】

　　学生回顾平面向量运算法则，推导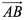和AB的中点坐标公式.

　　问题7：已知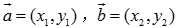，当两个向量平行时，它们的坐标应该满足什么条件？

　　【学生活动7】

　　学生利用平行向量基本定理推导公式，在此需要注意引导学生注意如何消掉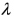？注意分母是否为0的讨论.

　　【设计意图】

　　向量的坐标表示为用“数”的运算处理“形”的问题搭起了桥梁，向量的坐标表示实际是向量的代数表示，使向量的运算完全代数化，为几何问题的解决又提供了一种方法．向量的坐标表示中，根据平面向量基本定理可选择特殊的基底将向量坐标化．因为学生理解向量与坐标间对应关系有些困难，所以先借助向量分解，更便于学生理解．在学生理解了向量的坐标表示后，后面的运算法则和各个公式都可以根据前面学习的平面向量的知识很轻松地推导出来.

　　二、例题讲解，深化理解

　　例1（课本162页例1）

　　如图所示，写出向量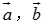的坐标.

　　变式：可以根据实际情况增加向量坐标的表示，特别是相等向量.（如图所示）

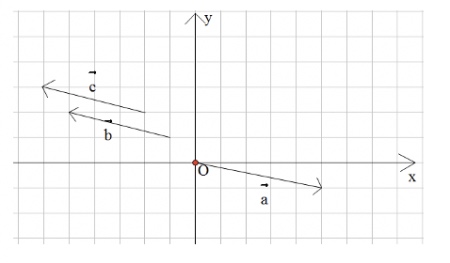
　　【设计意图】

　　为完成本节课的教学目标设计选用3道例题，让学生通过例题理解巩固平面向量的坐标表示，及各个坐标公式的熟练应用，一题多解、一题多练可以培养学生的解题思维的能力.

　　三、课堂练习，巩固所学

　　四、归纳总结：

　　1、平面向量的坐标的概念；

　　2、掌握向量的加法、减法、实数与向量的积的坐标运算法则，并能进行相关运算；

　　3、会根据平面向量的坐标，判断向量是否共线.