6.1.3向量的减法
教学课时:0.5课时
教学目标:
1.了解相反向量的概念.
2.掌握向量的减法,会作两个向量的减向量,并理解其几何意义.
3.通过阐述向量的减法运算可以转化成向量的加法运算,理解事物间可以相互转化的辩证思想.
4.通过本节学习,利用类比的方法探究向量减法的运算法则,培养探索精神与创新意识.
教学重点:
向量减法的概念和向量减法的作图法.
教学难点:
减法运算时方向的确定.
教学过程:
一、问题引入,尝试探究
问题:已知向量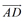 是向量
是向量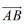 与向量
与向量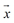 的和,如图所示,你能作出表示向量
的和,如图所示,你能作出表示向量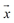 的有向线段吗?
的有向线段吗?
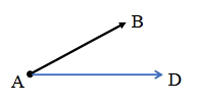
【学生活动】
【根据向量的加法动手操作】
1.在图中画出向量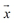 ;
;
2.检验所画出的向量是不是所求.
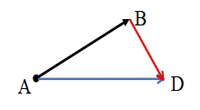
【设计意图】在向量加法的基础上引入减法定义和作图法则,符合学生认知规律,有利于减法运算的掌握.
二、向量的减法定义及表示
(一)、向量的减法定义及表示
1.定义:
一般地,平面上任意给定两个向量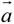 、
、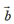 ,如果向量
,如果向量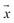 能够满足
能够满足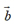 +
+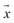 =
=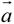 ,
,
则称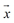 为向量
为向量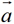 与向量
与向量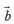 的差,并记作:
的差,并记作: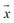 =
=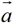 -
-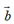 .
.
2.表示方法:
向量减法的三角形法则
当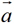 与
与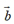 不共线时,
不共线时,
已知向量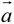 、
、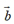 ,
,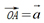 ,
,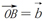 ,则由向量加法的三角形法则,得
,则由向量加法的三角形法则,得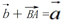 ,
,
我们把向量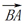 、叫做向量
、叫做向量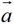 与
与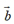 的差,记作:
的差,记作: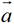 -
-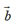 、即:
、即: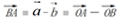 .
.
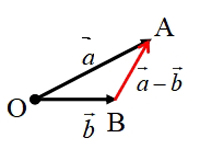
结论:
①如果把两个向量的始点放在一起,则这两个向量的差是以减向量的终点为始点,被减向量的终点为终点的向量;
②一个向量等于它的终点相对于点O的位置向量减去它的始点相对于点O的位置向量,简记为:“终点向量减始点向量”.
(二)、相反向量的定义
1.定义:
给定一个向量,我们把与这个向量方向相反、大小相等的向量称为它的相反向量,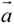 的相反向量记作:-
的相反向量记作:-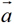 。
。
2.相关结论:

3.探究:
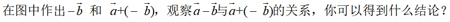
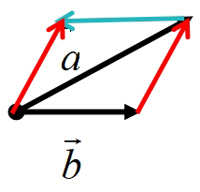
结论1: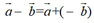 即:一个向量减去另一个向量,等于第一个向量加上第二个向量的相反向量.
即:一个向量减去另一个向量,等于第一个向量加上第二个向量的相反向量.
结论2:当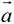 与
与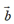 共线且方向相同时
共线且方向相同时
当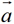 与
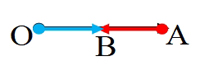
与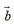 共线且方向相反时:
共线且方向相反时:
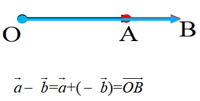
结论3:
【阶段小结】:分别研究在向量共线与不共线时的减法表示,验证减法定义.
【设计意图】数形结合,分类讨论了向量共线与不共线时的减法表示,并可以由图示得出相关结论:

为下面的例2的求解做好铺垫.同时,可以通过课后题加强图形中向量加减法的表示.
三、应用举例
例1:(课本143页例1)

解:如图所示,由向量的加法的平行四边形法则可知: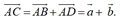
由向量的减法定义可知: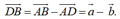
变式训练1(1):
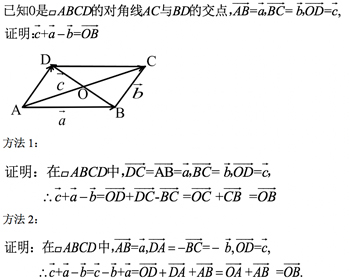
【设计意图】平行四边形是向量运算中经常遇到的图形,此题作为重点让学生熟练掌握.
【方法小结】:搞清楚图形中的相等向量、相反向量、平行向量以及构成三角形三向量之间的关系,确定已知向量与被表示向量的转化渠道.
变式训练1(2):

例2:(课本143页例2)

变式训练2:
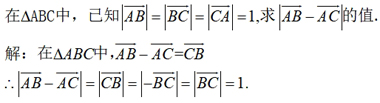
四、课堂练习,巩固所学

五、课堂小结、反思升华
知识小结:
1.向量减法的实质是向量加法的逆运算.即: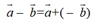
2.在用三角形法则作向量减法时,要注意“差向量连接向量的终点,箭头指向被减数”即: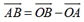
3.
思想方法小结:
数形结合、相互转化、类比
本网站旨在促进我国基础教育的信息交流,促进基础教育事业的发展。本网站转载的资料,如果作者不希望我们在网上使用其作品,请立即与我们联系,我们会在收到您的意见后立即从网上移除有关内容。未经人教网的明确书面许可,任何人不得复制或对人教网所属的服务器做镜像。

