6.1.2向量的加法
教学课时:1课时
教学目标:
1、掌握向量加法的三角形法则、平行四边形法则;
2、掌握向量加法的交换律、结合律,能够应用这些定律进行计算;
3、通过探究、思考、交流、解决问题等方式锻炼培养学生的逻辑思维能力、运算能力
教学重点:
向量加法的三角形法则、平行四边形法则及交换律、结合律的应用
教学难点:
理解向量加法的法则及其几何意义
教学过程:
一、设置情境,引入新课
情景1:假设某人上午从点A到达了点B,下午从点B到达了点C.
(1)分别用向量表示出该人上午的位移、下午的位移以及这一天的位移;
(2)这一天的位移与上午的位移、下午的位移有什么联系?试从大小和方向两个角度加以阐述.
情景2:从物理学中我们已经知道,力既有大小也有方向,因此力是向量.当在光滑的水平面上沿两个不同的方向拉动一个静止的物体时,物体会沿着力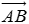 或
或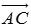 所在的方向运动吗?如果不会,物体的运动方向将是怎样的?
所在的方向运动吗?如果不会,物体的运动方向将是怎样的?
学生活动:
1.学生个人自主探究以上两个情景,得出向量加法运算的基本想法.
2.协作讨论形成向量加法运算的三角形法则和平行四边形法则.
二、知识形成1
知识点1:向量加法的三角形法则
(1)和向量:一般地,平面上任意给定两个向量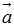 ,
,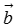 ,在该平面内任取一点A,作
,在该平面内任取一点A,作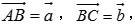 作出向量
作出向量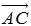 ,则向量
,则向量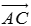 称为
称为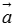 与
与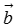 的和(也称
的和(也称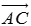 为向量
为向量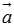 与
与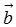 的和向量).向量
的和向量).向量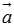 与
与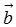 的和向量记作
的和向量记作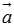 +
+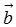 .
.
(2)和向量概念的给出既是加法的定义也是一种具体的做法.
(3)应用三角形法则,作图过程可以形象的记为是“尾首相连”,得到的和向量是“首尾相连”.
(4)特别地,当向量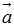 ,
,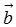 同向时,
同向时,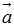 +
+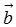 与
与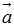 ,
,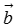 向量方向相同,模为
向量方向相同,模为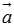 ,
,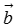 模的和,当
模的和,当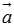 ,
,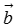 反向时,
反向时,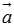 +
+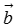 与
与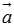 ,
,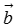 中模大的向量方向相同,模为
中模大的向量方向相同,模为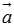 ,
,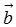 模差的绝对值.
模差的绝对值.
(5)模不等式: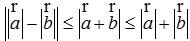 ,借助三角形两边之差和两边之和给出证明.
,借助三角形两边之差和两边之和给出证明.
知识点2:向量加法的平行四边形法则
(1)平行四边形法则,作图过程要求两个向量起点相同,和向量是同起点的对角线.
(2)平行四边形法则易得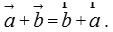
(3)平行四边形法则和三角形法则关系密切,可以相互转化.
【设计意图】
从教材给出两种法则计算向量加法的方法中对比可知,三角形法则既是和的给出定义,同时又是一种做法,而平行四边形法则的给出通过已学过的物理知识进行引入,巩固了学生对于向量加法的定义,同时又给出了另一种计算法则。两种方法是有密切联系的,完成知识形成后可以将两种法则的转换给出,以便加深理解。
三、例题讲解,深化理解1

【设计意图】
通过具体事例让学生能够理解三角形法则,同时也能够将特殊情况融入到计算之中,有利于理解和应用三角形法则.
四、知识形成2
学生活动:通过三角形法则和平行四边形法则,对照教材140页内容,归纳多个向量相加的计算法则.
知识点3:多个向量的加法
(1)结合律: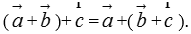
(2)多边形法则:将所有求和的向量依次首尾相连,和向量是以第一个向量的始点为始点,最后一个向量的终点为终点的向量.
【设计意图】
教材中是先作图说明了三个向量结合律的成立,同时作图的过程可以帮助学生总结多边形法则,有了多边形法则,反过来也可以很好的说明结合律是成立的.
五、例题讲解,深化理解2
例2(课本141页例2)化简下列各式:
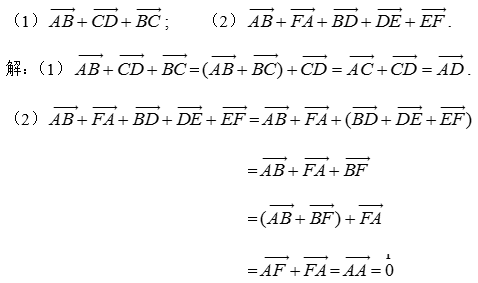
【设计意图】
多个向量在化简求和的过程中,结合律和交换律的作用是非常大的,能够非常有效的进行计算.
六、课堂练习,巩固所学
1、(课本141页练习A第2题)已知A,B,C是三角形ABC的三个顶点,求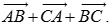
参考答案: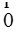
2、(课本141页练习A第3题)已知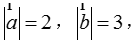 求
求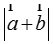 的最大值和最小值,并说明取得最大值和最小值时
的最大值和最小值,并说明取得最大值和最小值时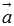 ,
, 的关系.
的关系.
参考答案:最大值5,最小值1.
七、归纳总结:
1、三角形法则、平行四边形法则的应用;
2、多个向量相加的法则;
3、交换律和结合律在计算中的应用.
本网站旨在促进我国基础教育的信息交流,促进基础教育事业的发展。本网站转载的资料,如果作者不希望我们在网上使用其作品,请立即与我们联系,我们会在收到您的意见后立即从网上移除有关内容。未经人教网的明确书面许可,任何人不得复制或对人教网所属的服务器做镜像。

