6.1.4数乘向量
教学课时:0.5课时
教学目标:
1.了解数乘向量的定义.
2.通过数乘向量的定义,掌握并理解其几何意义.
3.通过数乘向量的学习会判断两向量平行及三点共线问题.
教学重点:
数乘向量定义及其几何意义的理解.
教学难点:
利用数乘向量判断两向量平行及处理三点共线问题.
教学过程:
一、问题引入,尝试探究
多个向量相加,结果是一个向量。特别地,给定一个向量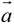 ,三个向量
,三个向量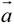 相加的结果,是一个模为
相加的结果,是一个模为 ,方向与
,方向与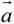 相同的向量.你能根据上述实例,给出一个实数
相同的向量.你能根据上述实例,给出一个实数 与任意一个向量
与任意一个向量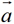 的乘积
的乘积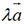 的定义么?
的定义么?
结论:
一般地,给定一个实数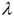 与任意一个向量
与任意一个向量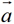 ,规定它们的乘积是一个向量,记作
,规定它们的乘积是一个向量,记作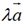 ,其中:
,其中:
(1)当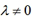 且
且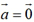 时,
时,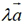 的模为
的模为 ,而且
,而且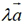 的方向如下:
的方向如下:
①.当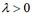 时,与
时,与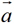 的方向相同;
的方向相同;
②.当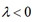 时,与
时,与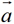 的方向相反.
的方向相反.
(2)当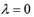 或
或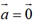 时,
时,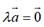 .
.
教师引导学生回答下面问题.
数乘向量几何意义:
上述实数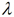 与向量
与向量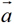 相乘的运算简称为数乘向量.由定义不难看出,数乘向量结果是一个向量,而且与原来的向量共线(平行);数乘向量的几何意义是,把向量沿着它的方向或者反方向放大或者缩小,特别地,一个向量的相反向量可以看成-1与这个向量的乘积,即
相乘的运算简称为数乘向量.由定义不难看出,数乘向量结果是一个向量,而且与原来的向量共线(平行);数乘向量的几何意义是,把向量沿着它的方向或者反方向放大或者缩小,特别地,一个向量的相反向量可以看成-1与这个向量的乘积,即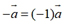 .
.
向量数乘的结合律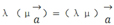 ;向量共线的判断;三点共线问题的证明方法
;向量共线的判断;三点共线问题的证明方法
二.应用举例、典型例题

【设计意图】在理解数乘向量基础上,适当增加两个例题,符合学生认知规律,有利于对数乘运算的掌握.
三.课堂练习,巩固新知
1.(课本146页练习A2)化简下列各式:
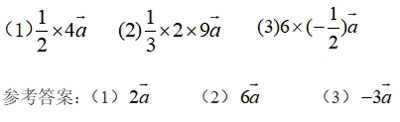
2.(课本147页练习B1)已知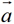 是非零向量,实数
是非零向量,实数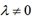 ,判断下列命题的真假:
,判断下列命题的真假:
(1)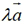 与
与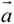 的方向一定相同;
的方向一定相同;
(2)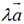 与
与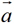 的方向相反的充要条件是
的方向相反的充要条件是 .
.
参考答案:(1)假 (2)真
3.(课本147页练习B4)已知四边形ABCD为平行四边形,AC与BD相交于O,设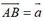 ,
,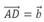 ,试用向量
,试用向量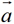 ,
,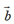 表示,
表示,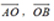 .
.
参考答案:(1)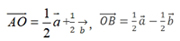
【设计意图】追加三个练习题,增强学生对数乘向量的理解,有利用学生对知识的进一步掌握.
四、归纳总结:
1.数乘向量的定义.
2.数乘向量的几何意义.
3利用数乘向量判断两向量平行及处理三点共线问题.
本网站旨在促进我国基础教育的信息交流,促进基础教育事业的发展。本网站转载的资料,如果作者不希望我们在网上使用其作品,请立即与我们联系,我们会在收到您的意见后立即从网上移除有关内容。未经人教网的明确书面许可,任何人不得复制或对人教网所属的服务器做镜像。


~206679194-215dcd4664964991b08a5d136188baf0~~~~~~www.pep.com.cn~110000008~sys_200001~11~www.pep.com.cn/gzsxb/xrjbgzsxb/xrjgsbwd/202106/t20210618_1968162.html~~~206679194-68a6d40148ab4b3a8d5382eaf6cd4008~~)