教学课时：1课时

　　教学目标：

　　1、理解向量线性运算的定义和运算法则，会进行向量的线性运算.

　　2、理解两个向量共线的含义，能利用共线的条件解决相关问题.

　　3、让学生在解题过程中体会数形结合的思想，训练学生数学抽象、数学运算的学科素养.

　　教学重点：

　　线性运算法则的灵活应用.

　　教学难点：

　　线性运算法则的灵活应用.

　　教学过程：

　　一、提出问题，解决问题：

　　问题：向量的加法和数乘向量的结果是向量吗？能进行混合运算吗？

　　规定：一般地,一个含有向量加法、数乘向量运算的式子,要先算数乘向量,再算向量加法.

　　【思考】：

　　（1）向量的加法与数乘向量能进行混合运算的根本原因是什么？

　　提示：向量的加法与数乘向量的结果仍是一个向量.

　　（2）这里的条件“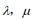为实数”能省略吗？为什么？

　　提示：不能,数乘向量中的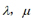都是实数,只有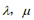都是实数时,运算律才成立.

　　【学生活动1】

　　通过阅读课本第147，148页例1上面的内容，让学生解释两个运算律成立的原因.

　　向量的线性运算：向量的加、减、数乘向量以及它们的混合运算,统称为向量的线性运算.

　　注：向量的线性运算，规定先计算数乘向量，再按从左往右的顺序进行运算，若有括号，先算括号内各项.

　　【素养小测】思维辨析（对的打“√”,错的打“×”）

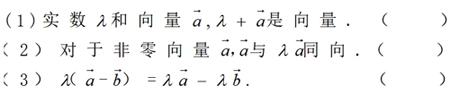
　　【设计意图】

　　学生前面已经学习了向量的加法、减法、数乘，在巩固复习的基础上再引入新课题，让学生通过以前学习的知识解释运算律成立的原因，再进行运算律的应用，知识点与具体题目结合，从而得以使学生灵活运用知识.

　　二、例题讲解，深化理解

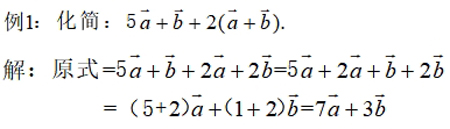
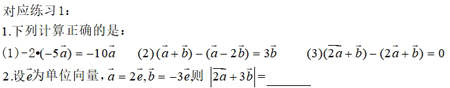
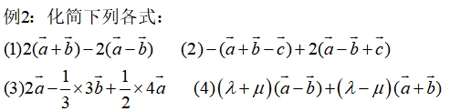
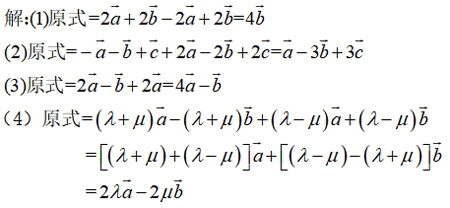
　　【思维·引】1.类比实数运算中合并同类项的方法化简.

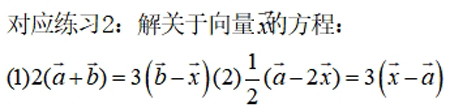
　　【思维·引】2.向量也可以通过列方程来解,把所求向量当作未知数,利用解代数方程的方法求解,同时在运算过程中要多注意观察,恰当运用运算律,简化运算.

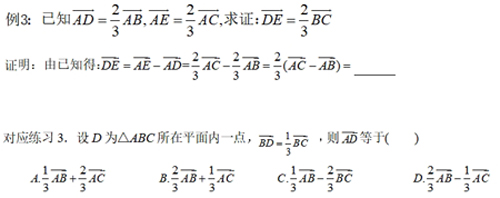
　　【思维·引】3.用已知向量表示未知向量的技巧

　　（1）由已知向量表示未知向量时,要善于利用三角形法则、平行四边形法则以及向量线性运算的运算律.

　　（2）当直接表示较困难时,应考虑利用方程（组）求解.

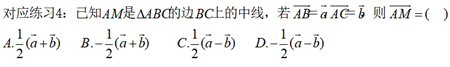
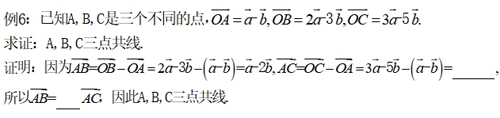
　　【思维·引】5.证明三点共线,往往要转化为证明过同一点的两个有向线段表示的向量共线,必须说明构造的两个向量有公共点,否则两向量所在的基线可能平行,解题时常常会因忽视对公共点的说明而丢分.

　　对应练习5.如图所示，在平行四边形ABCD中，点M是AB的中点，

　　【设计意图】增加学生对运算律的理解和对所学知识的复习.

　　三、课堂练习，巩固所学

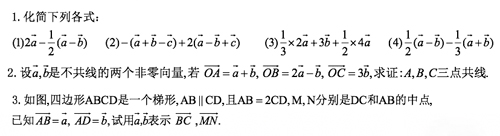
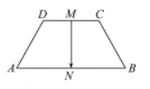
　　四、归纳总结：

　　1.理解向量线性运算的意义及运算法则，会进行向量的线性运算.

　　2.掌握用已知向量表示未知向量的方法.

　　3.掌握证明三点共线的方法.