教学课时：第1课时

　　教学目标：

　　1.通过事例使学生认识对数的模型，体会引入对数的必要性，理解对数的概念，及常用对数和自然对数；

　　2.通过观察分析得出了解对数运算与指数运算互逆关系，掌握对数式与指数式的互化，理解对数的性质；

　　3.通过教学培养学生类比、分析、转化、抽象概括能力，提高理解和运用数学符号的能力。

　　教学重点：

　　引入对数的定义，熟练掌握指数式与对数式的互化。

　　教学难点：

　　理解对数的概念和性质。

　　教学过程：

　　一、情境与问题

　　请学生根据所学的指数函数的知识完成下表：（表格是开放性的，学生可以填写自己认为正确的数字）

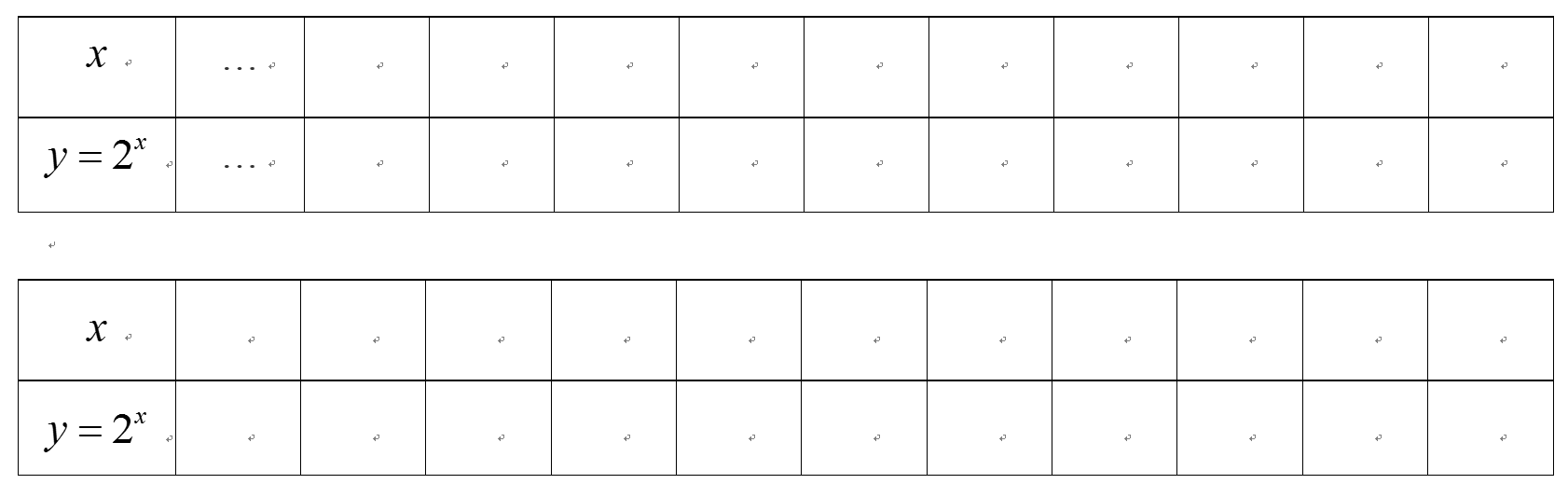
　　观察学生填表，教师再给出示范：

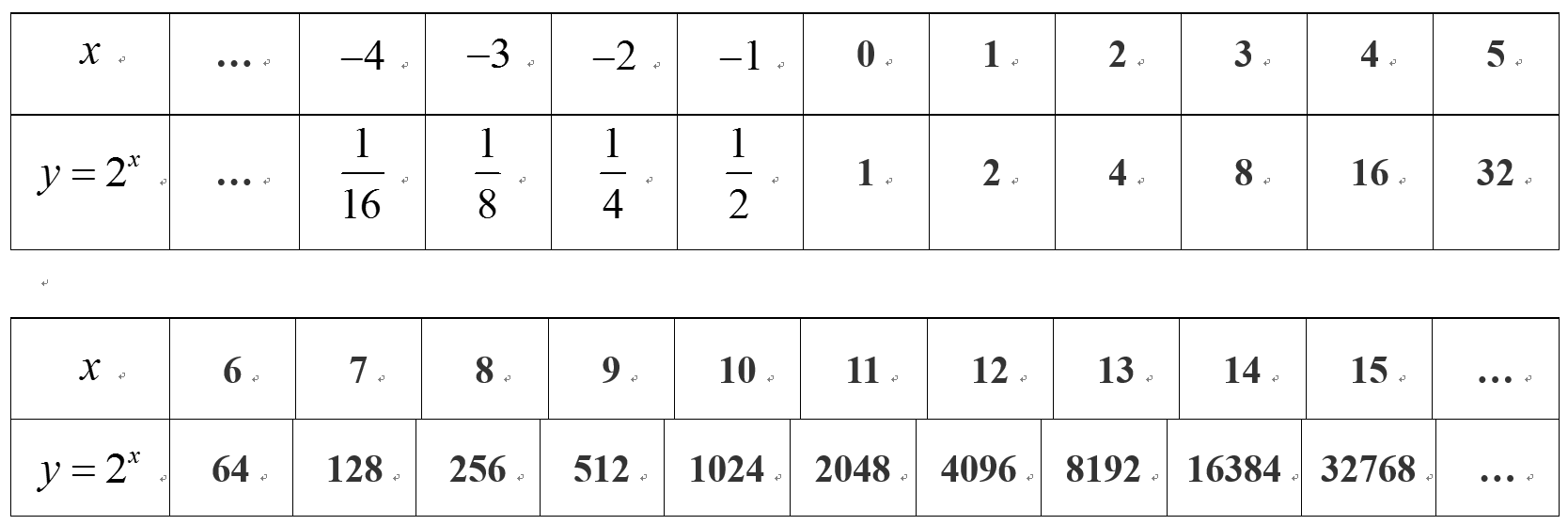
　　方程2^x=128的一个实根是____________；（解答：x=7）

　　尝试与发现：（1）若2^x=1/32，则x=____________；（解答：-5）

　　        （2）若2^x=3，则x=____________；

　　（教师引导学生观察指数函数的图像寻找、估计方程中x的大小）

　　（3）在函数y=a^x（a＞0且a≠1）中，我们将幂指数x叫做以a为底y的对数。

　　因此，（1）中-5是以2为底1/32的对数，那么,（2）中x是以2为底3的对数。

　　思考2：满足2^x=3的x的值，我们用log₂3表示，即x=log₂3，并叫做“以2为底3的对数”。那么满足2^x=16，4^x=8的x的值可分别怎样表示？

　　思考3：一般地，如果a^x=N（a＞0且a≠1），那么数x叫做什么？怎样表示？

　　【设计意图】

　　回顾指数函数的概念，根据指数函数的图像和性质，列表研究方程中未知数的各种情形，引入对数的概念，激发学生学习对数的兴趣，培养对数学习的科学研究精神。

　　二、新课讲授

　　1.对数的定义

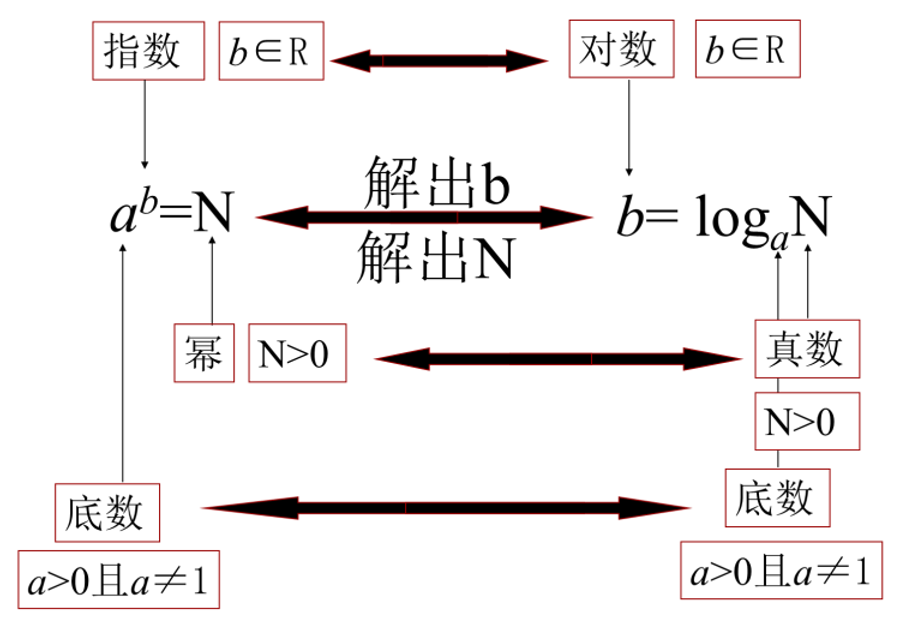
　　一般地，如果a^b=N（a＞0,a≠1），那么数b叫做以a为底N的对数（Logarithm），记作：log_aN，即b=log_aN，其中，a—底数，N—真数，log_aN—对数式。

　　思考4：（1）在对数log_aN中N有范围限定吗？为什么？

　　     （2）log_a(-2)、log₂0有没有意义？

　　说明：（1） 注意底数的限制a＞0，且a≠1；

　　    （2）负数和零没有对数；

　　    （3）注意对数的书写格式。

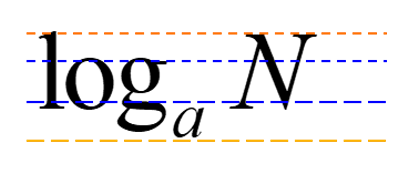
　　【设计意图】正确理解对数定义中底数的限制，为以后对数型函数定义域的确定作准备。

　　2.对数式与指数式的互化

　　我们可以由指数式得到对数式，也可以由对数式得到指数式：

　　把下列指数式改写成对数式：

　　7²=49，5⁰=1，9^-1/2=1/3

  把下列对数式改写成指数式：

   log₂1/8=-3，log₄8=2/3

　　3.深入理解对数的定义

　　（1）对数式书写的格式，体会log_a(x+1)与log_ax+1的区别；

　　（2）对“log”的理解：就像我们在初中阶段引入“√，sin”等数学符号一样，是一个新的数学运算符号；

　　（3）回想：√5的数学含义： ①它表示一个非负实数；②它的平方等于5；

　　同理，log₂3这一数学符号的含义：

　　① 它表示一个实数；② 以2为底，这个实数做指数所得的幂的值恰好为3。

　　同理，log_aN这一数学符号的含义：

　　① 它表示一个实数；② 以a为底，这个实数做指数所得的幂的值恰好为N。

　　（4）实质上，对数表达式是指数式的另一种表达形式。

　　4.两个重要对数

　　思考5： 满足10^x=N，e^x=N（其中e=2.7182818459045…）中的x的值可分别怎样表示？这样的对数有什么特殊名称？

　　说明：（1）常用对数（common logarithm）：以10为底的对数lgN；

　　    （2）自然对数（natural logarithm）：以无理数e=2.71828…为底的对数的对数lnN。

　　求值：

　　lg0.01=____________；lg100=____________；ln10=____________。

　　【设计意图】学会表达特殊底的对数，并感受对数的大小，为以后对数运算的准确作好准备。

　　三、探究活动、感悟数学

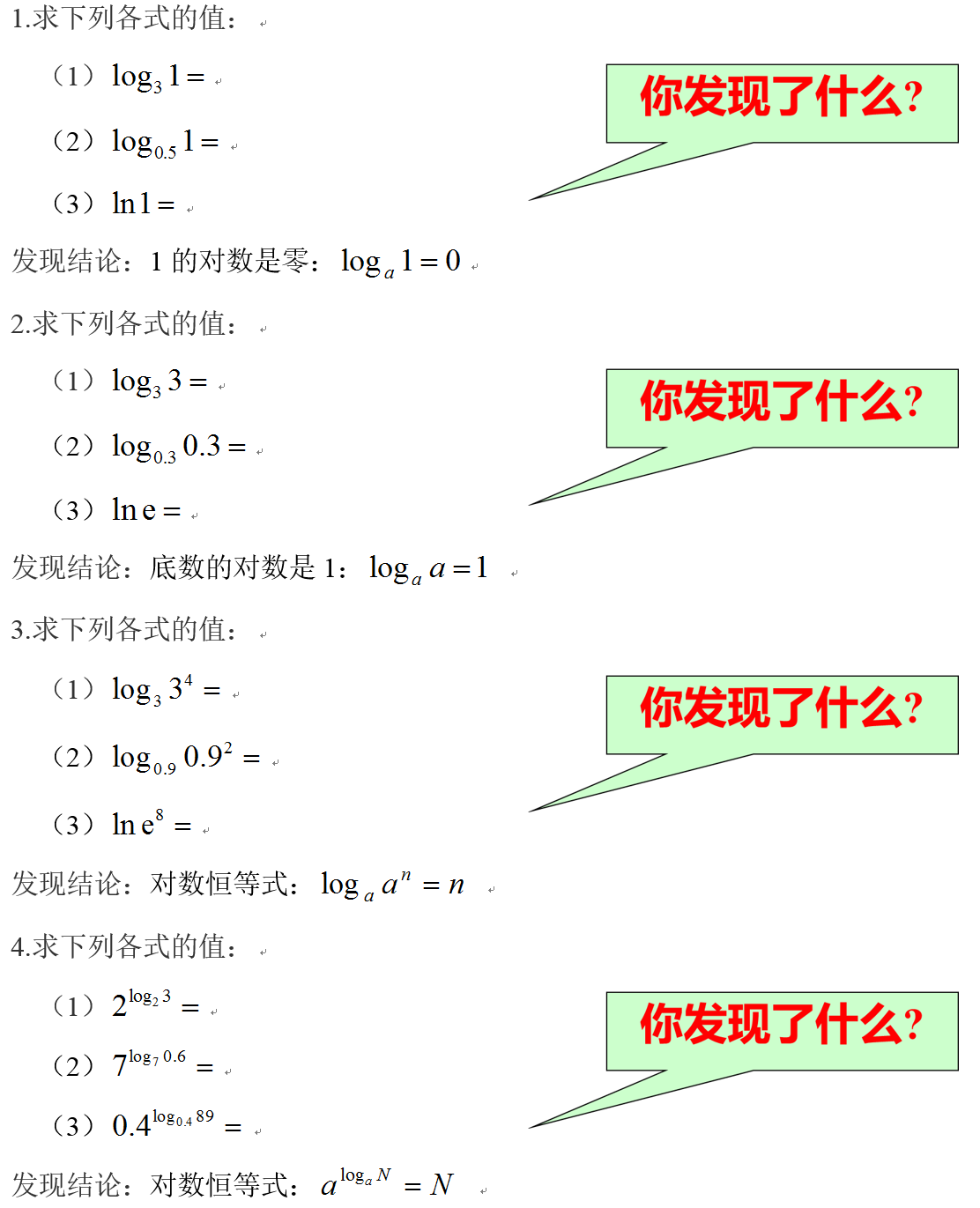
　　【设计意图】让学生独立思考完成对数性质的研究，

　　归纳总结：（1）负数和零没有对数；

　　       （2）1的对数是零：log_a1=0；

　　       （3）底数的对数是1：log_aa=1；

　　       （4）对数恒等式：log_aaⁿ=n；

　　       （5）对数恒等式：a^logaN=N。

　　四、课堂练习

   思考6：生物机体内碳14大约以每年0.012%衰减，湖南长沙马王堆文物出土时碳14的残余量约是原始含量的76.7%，试推测马王堆古墓距今有多少年？

　　【设计意图】建立对数模型，解决实际问题，让整节课从问题开始，又回到问题解决中去，使学生在课堂上不断思考新的问题，学会对数学概念展开学习的方法。

　　五、对数的文化意义

　　对数发明是17世纪数学史上的重大事件，为对数的发明与解析几何的创立、微积分的建立是17世 纪数学史上的3大成就。 伽利略说，给我空间、时间及对数，我可以创造一个宇宙。 布里格斯（常用对数表的发明者）说，对数的发明，延长了天文学家的寿命。

　　对数的发明让天文学家欣喜若狂，这是为什么？我们将会发现，对数可以将乘除法变为加减法，把天文数字变为较小的数，简化数的运算。这些都非常有趣。在下一节课我们还将一起来探究对数的运算。

　　六、课堂小结

　　1.引入对数的必要性，关键是对数定义；

　　2.指数与对数的关系，重点指数式与对数式互换；

　　3.对数的基本性质，学会求值。

　　4.本节课知识导图：

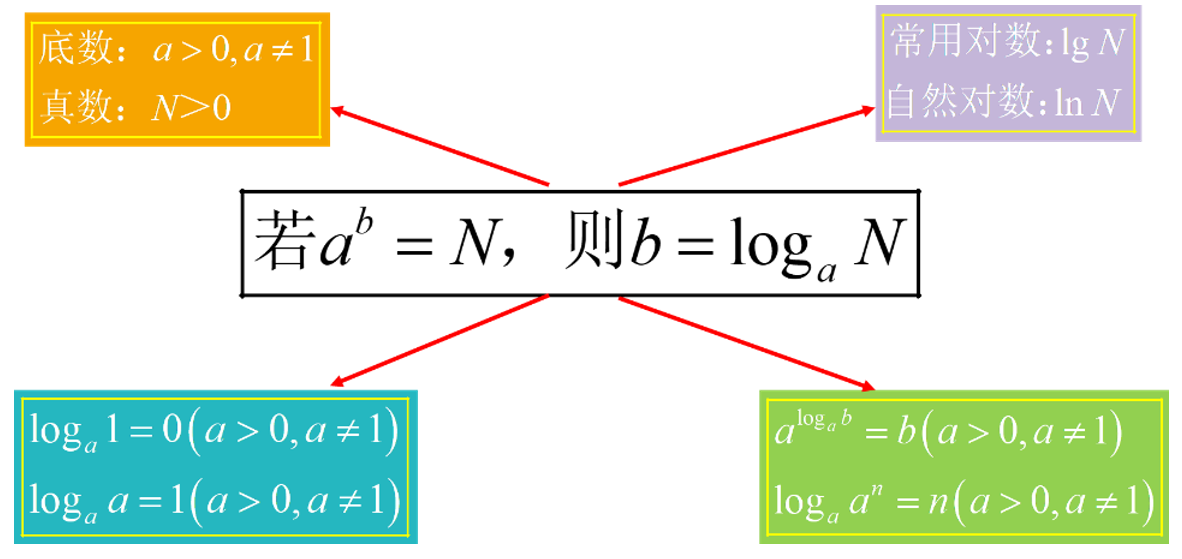
　　六、布置作业

　　1.阅读课本第17页拓展阅读“对数发明起源的简介”和第18页拓展阅读“素数个数与对数” ；

　　2.课本第19页习题B。