教学课时：第2课时

　　教学目标：

　　1.体验通过数字的乘、除运算发现对数的运算法则的过程，掌握对数的运算法则，并会简单应用；

　　2.理解用换底公式将一般对数转化成自然对数或常用对数，掌握对数的综合运算；

　　3.了解对数的发现历史以及对简化运算的作用，经历数学运算法则的发现、论证、提炼过程，提升数学运算、数学抽象的核心素养.

　　教学重点：

　　对数的运算性质，用换底公式将一般对数转化成自然对数或常用对数.

　　教学难点：

　　对数的运算法则和换底公式的熟练运用.

　　教学过程：

　　一、情境与问题

　　回顾：根据所学的指数函数的知识完成下表：（上节课的表格）

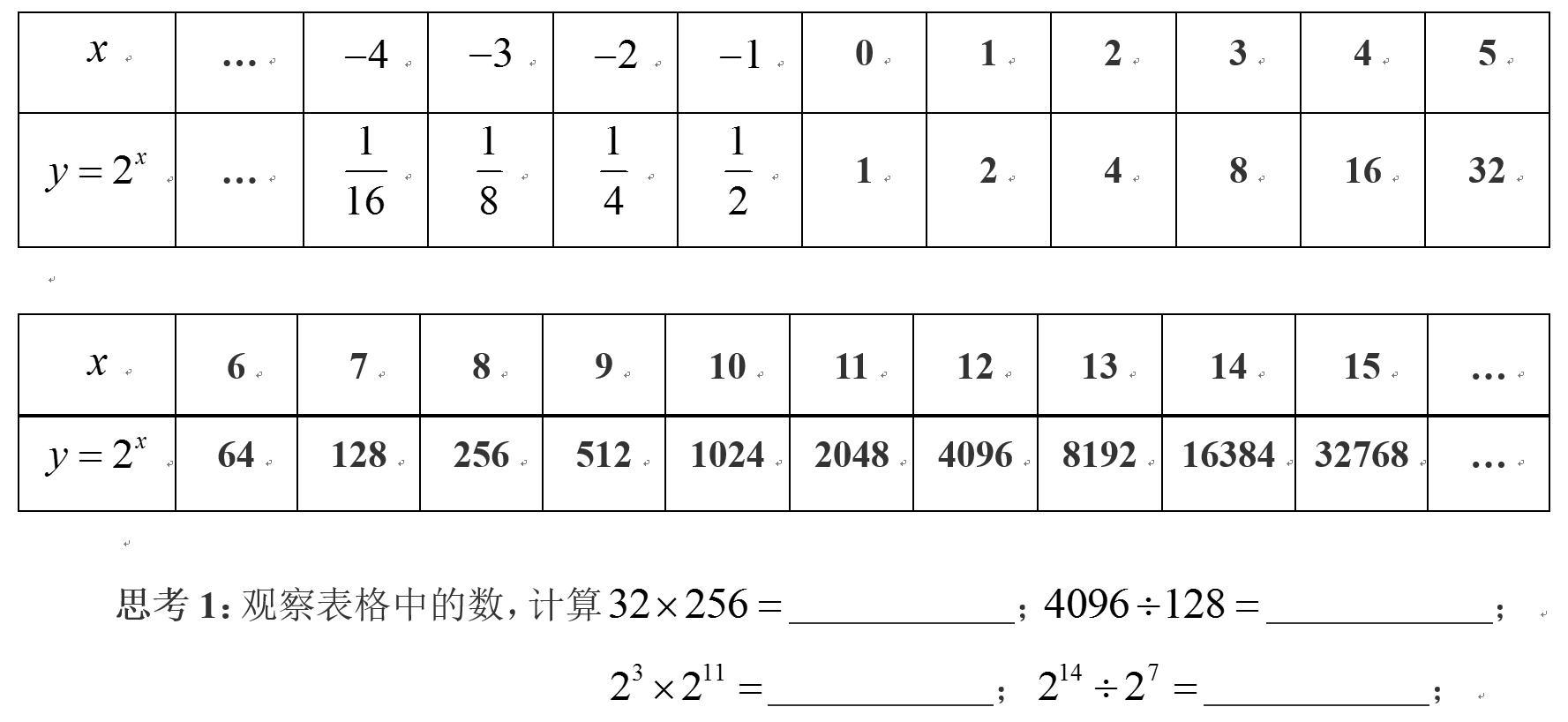
　　学生独立思考完成解答，教师组织学生讨论评析，进行归纳总结概括得出对数的运算法则，并引导学生类比、推导其他运算法则。

　　由同底数的幂的指数和对数的互相转化关系可猜想：（设a^a=M，a^B=M，a>0，a≠1）

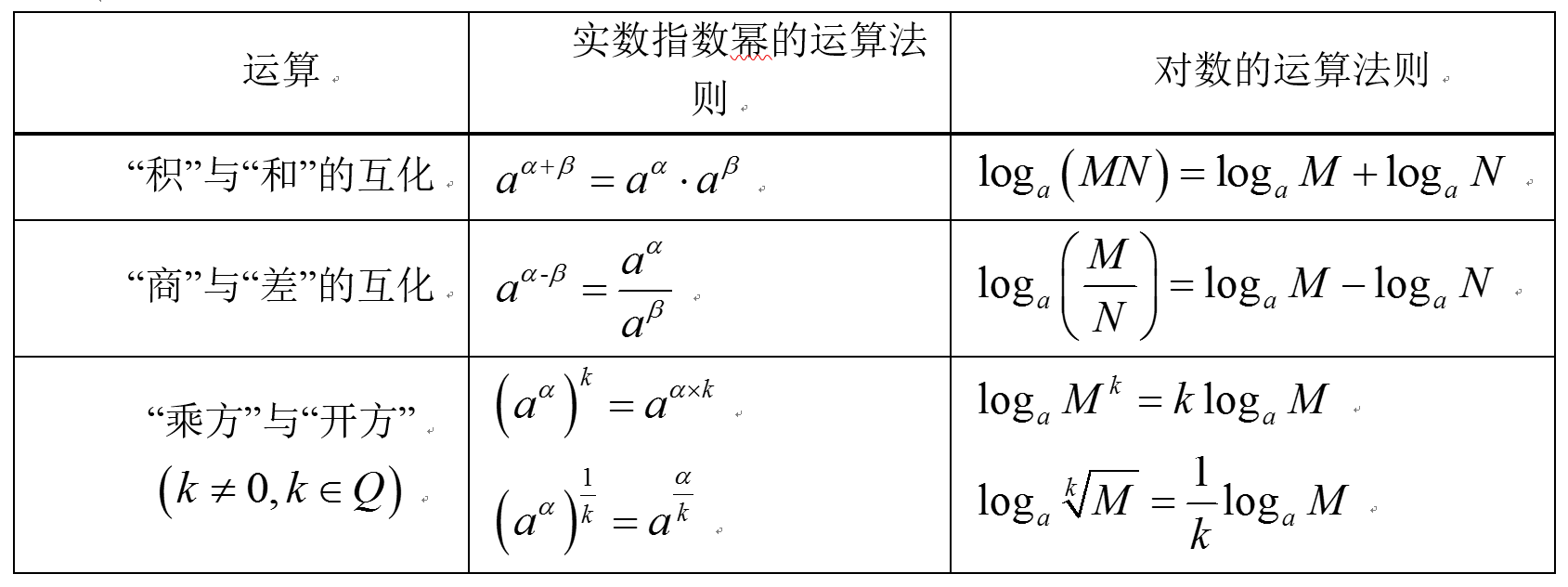
　　组织学生论证猜想，具体要求：

　　（1）请各组同学选一个猜想的命题，判断它的正确性，并给出证明

　　（2）各组派一名代表的同学汇报　　

　　【设计意图】体验通过数字的乘、除运算发现对数的运算法则的过程，是学生经历数学运算法则的发现、论证、提炼的过程，提升数学运算、数学抽象的核心素养.

　　二、对数的运算法则

　　【设计意图】通过小组讨论、论证猜想、小组汇报等环节，使学生个科学的态度研究数学问题和数学法则，引导学生用自然语言叙述上面的三个运算法则，通过展示错误的运算，提醒学生正确掌握对数的运算性质。

　　三、课堂练习

　　题型一 对数运算性质的应用

　　说明：（1）简易语言表达:”积的对数=对数的和”……；

　　（2）有时可逆向运用公式；

　　（3）真数的取值必须是（0，+∞）；

　　（4）注意正确理解对数的运算法则.

　　【设计意图】在应用过程中进一步理解和掌握对数的运算法则，在练习中反馈学生对对数运算法则掌握的情况，巩固所学知识。

　　思考2：（1）对数运算性质的实质是什么？

　　（2）运用对数运算性质时应注意什么？

　　对数运算性质的实质是可以把乘、除、乘方、开方的运算转化为对数的加、减、乘运算，从而降低了运算难度，加快了运算速度，简化了计算方法。

　　运算性质只有当M>0，N>0，a>0且a≠1时才有意义。

　　思考3：

　　问题：对数的运算法则仅适用于对数的底数相同的情形，若在解题过程中，遇到对数的底数不相同时怎么办？

　　【设计意图】深入研究对数的运算法则，针对同底的对数运算与不同底的对数运算进行分类讨论，启发学生将不同底对数转化为同底的对数运算的想法，引出换底公式。

　　四、换底公式

　　注意：

　　（1）换底公式成立的条件是公式中的每一个对数式都有意义；

　　（2）换底公式的意义在于改变对数式的底数，把不同底数的问题转化为同底数的问题进行计算、化简或证明；

　　（3）换底公式在实际应用中究竟换成以什么为底数，要由具体的已知条件来确定，一般换成以10为底的常用对数。

　　重要公式：换底公式常见的两种变形：

　　（1）log_ab*log_ba=1，表示真数与底数互换，所得对数值与原对数值互为倒数；

　　（2）log_NⁿM^m=m/nlog_NM ，表示对数的底数变为原来的n次方，真数变为原来的m次方，所得的对数值等于原来对数的m/n倍.

　　【设计意图】学生根据对数的定义推导对数的换底公式，了解换底公式的推导过程与思想方法，深刻理解指数与对数的关系。

　　五、强化练习

　　题型二 换底公式的应用

　　求值： (log₃2+log₉2)(log₄3+log₈3) 

　　练习：求下列各式的值

　　（1）(log₄3+log₈3)log2/log3

　　（2）(log₂125+log₄25+log₈5)(log₅2+log₂₅4+log₁₂₅8) 

　　拓展：用log_ax，log_ay，log_az表示下列各式：

　　题型三 对数的综合应用

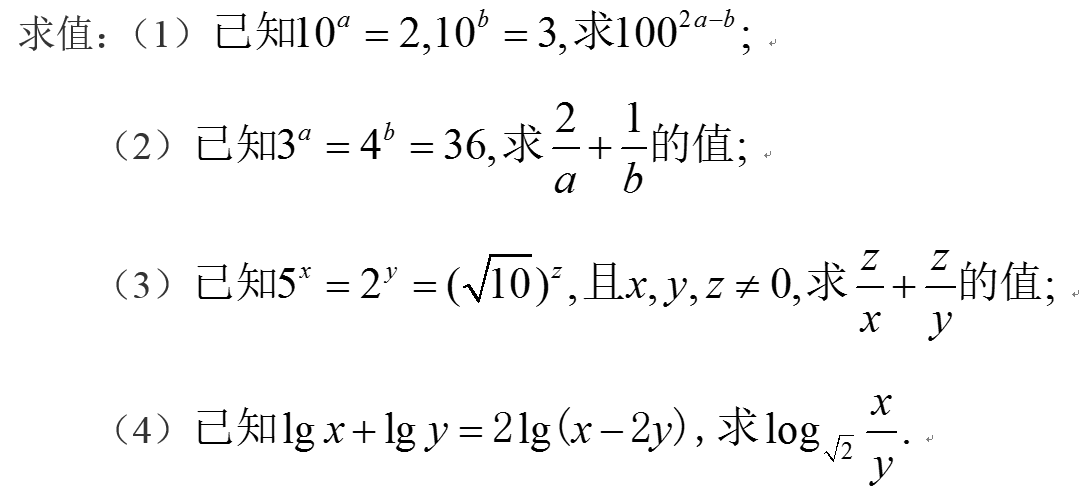
　　【设计意图】利用换底公式解题时常常换成常用对数，但有时还要根据具体题目确定底数。

　　六、课堂小结

　　1. 对于底数相同的对数式的化简或求值，常用的方法是：

　　（1）“收”，将同底的对数的和（差）收成积（商）的对数；

　　（2）“拆”，将积（商）的对数拆成对数的和（差）。

　　对数的化简或求值一般是正用或逆用公式，对真数进行处理。选哪种策略化简，取决于问题的实际情况，一般本着便于真数化简的原则进行。

　　2. log_a1=0，log_aa=1（a>0，且a≠1）在计算对数值时经常用到。

　　七、布置作业

　　课本第23页练习A第1.2.3题；B第1—6题。