4.7 数学建模活动:生长规律的描述
教学课时:第1课时
教学目标:
1、经历从实际问题建立数学模型、运算求解、验证模型、改进模型的全过程,掌握建模方法以及论文写作方法,培养数学建模、数学运算等核心素养;
2、在数学建模过程中,选择适当的拟合函数,巩固函数概念以及对基本初等函数增长速度的比较与甄别,渗透待定系数法与方程思想。
教学重点:
数学建模的全过程。
教学难点:
选择适当的拟合函数与改进模型。
教学过程:
一、发现问题、提出问题
生物的生长发育是一个连续的过程,但不同的时间段可能有不同的增长速度。
卫生部2009年6月发布的《中国7岁以下儿童生长发育参照标准》指出,我国7岁以下女童身高(长)的中位数如下表所示(0岁指刚出生时):
|
年龄/岁 |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
|
身高/cm |
49.7 |
66.8 |
75 |
81.5 |
87.2 |
92.1 |
96.3 |
|
年龄/岁 |
3.5 |
4 |
4.5 |
5 |
5.5 |
6 |
6.5 |
|
身高/cm |
99.4 |
103.1 |
106.7 |
110.2 |
113.5 |
116.6 |
119.4 |
交流与讨论1:
①这个问题中涉及到两个量——年龄和身高,你能否用自己的语言描述这两个量之间的关系?
②这两个量之间的关系是不是函数关系?为什么?
③如果是函数关系,哪个是自变量?哪个是因变量?定义域和值域分别是什么?有什么性质?你能否写出一个函数解析式表示这个关系?
【设计意图】
从实际问题出发,引导学生发现问题、提出问题,从概念及表示方法上引导学生深入思考,为解决问题作一铺垫。
二、分析问题、建立模型
交流与讨论2:
①你认为怎样选择函数模型来刻画年龄和身高之间的变化关系?
我们可以先画出它的图像,从直观上看看像什么函数:
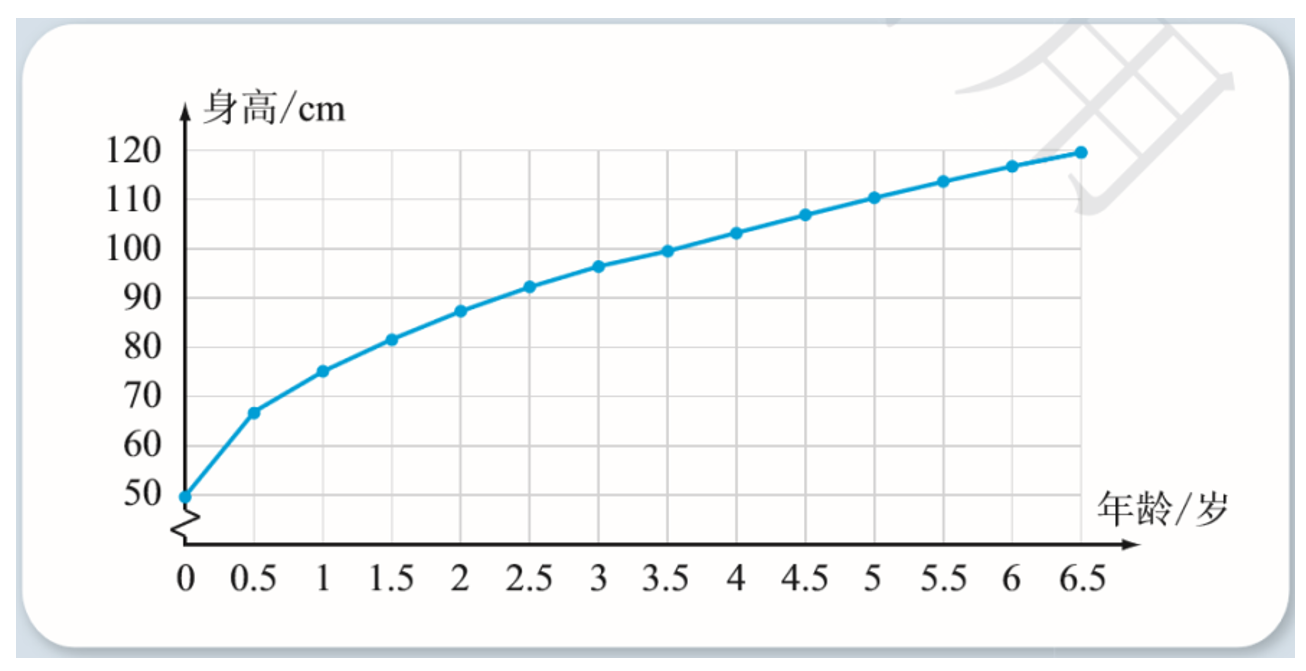
②我们学过一些什么函数?
预设答案:幂函数(包括一次函数、二次函数、反比例函数等)、指数函数、对数函数.还可能会答:分段函数。
③你觉得这个图像最像什么函数的图像?你能大概写出它的解析式吗?
预设答案:幂函数、对数函数。教学中,结合函数图像变换,进一步引导学生写出函数解析式的待定形式:f1(x)=axm/n+b, f2(x)=bloga(x+1)+c(a>1)。还可引导学生思考:指数函数 与这两个模型相比呢?
【设计意图】
从列表法到图像法表示函数,再到解析法表示函数,进一步巩固用函数刻画生长变化规律基本思路——用解析式来拟合数据与图像,这是一个逆过程,需要直观选择、模型对比、调整改进.为后面运算求解模型、改进模型埋下伏笔。
三、确定参数,计算求解
交流与讨论3:
①如果选择f1(x)=axm/n+b,你怎么确定指数m/n?怎么确定a和b?如果选择f2(x)=bloga(x+1)+c(a>1),你怎么确定底数a和系数b?
②请大家选择一个函数模型,各自选择适当的数据求出函数解析式。
③分别针对同一个函数模型的求解结果进行交流、对比,借助图像,凭直觉初步感知同一模型不同结果的优劣,以及不同模型刻画数据的优劣。
【设计意图】
通过选择不同的函数模型,以及选择同一函数模型而选择不同的数据求出待定系数,让学生体会拟合过程需要改进的必要性。
四、验证结果、改进模型
因为我们在求函数解析式时,都只用到了部分已有数据,而其它数据一般不可能与所求出的解析式完全吻合,所以我们需要验证所建立的函数模型的优劣。
交流与讨论4:
①你认为怎么验证函数模型?(从上述两类函数模型中,选择大家认为拟合较好的两个函数f1(x)和f2(x),列表、画图像,验证函数模型。)
预设答案:一是从已有数据中找出没有使用的数据代入函数解析式,看误差有多大,或者直接列成下表,将函数值与原有数据一一比对;二是在原来的图像中再画出所求函数的图像,看两个图像的偏差有多大。
|
年龄/岁 |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
|
身高/cm |
49.7 |
66.8 |
75 |
81.5 |
87.2 |
92.1 |
96.3 |
|
f1(x) |
|
|
|
|
|
|
|
| f2(x) |
|
|
|
|
|
|
|
|
年龄/岁 |
3.5 |
4 |
4.5 |
5 |
5.5 |
6 |
6.5 |
|
身高/cm |
99.4 |
103.1 |
106.7 |
110.2 |
113.5 |
116.6 |
119.4 |
| f1(x) |
|
|
|
|
|
|
|
| f2(x) |
|
|
|
|
|
|
|
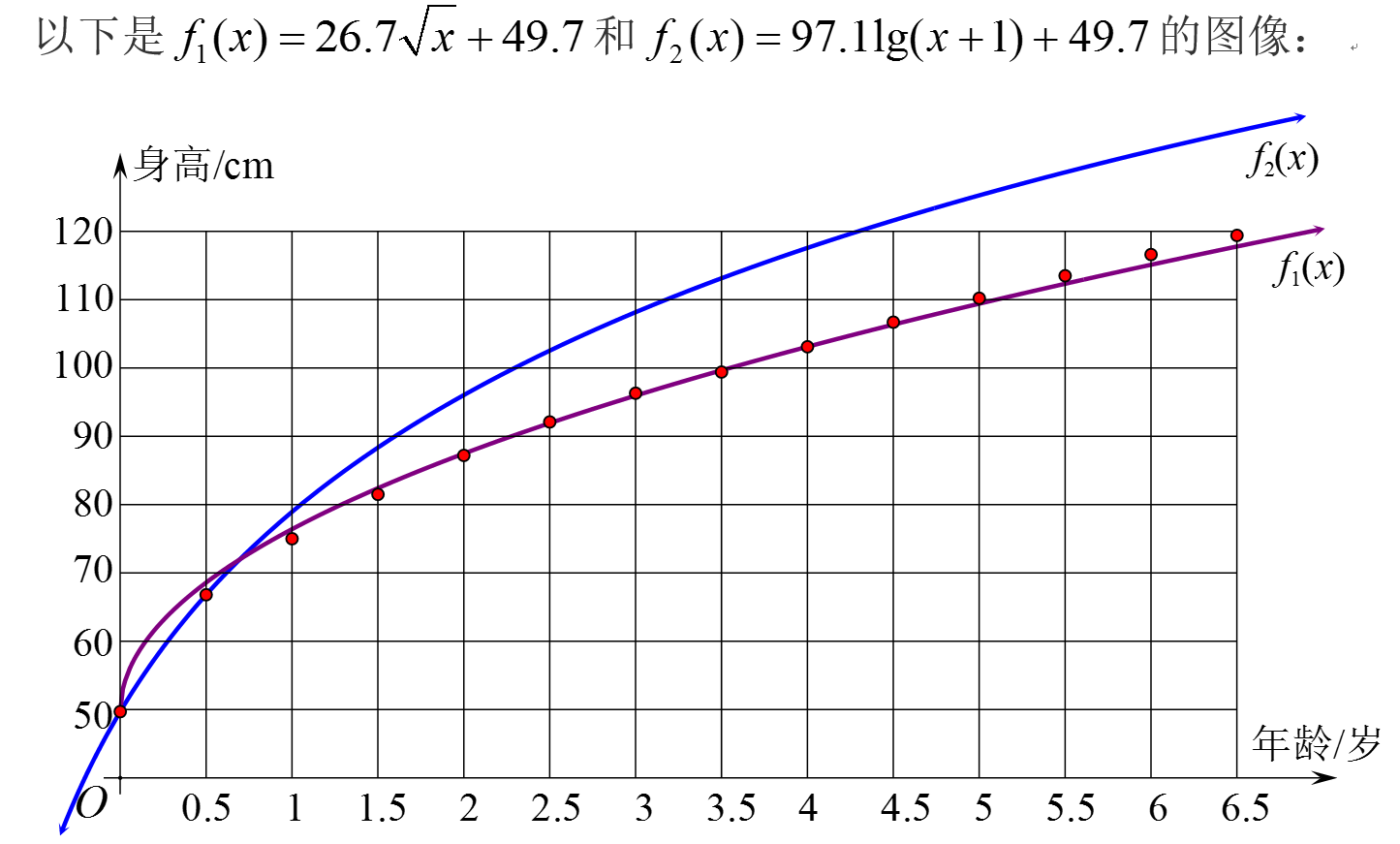
②你认为应该从哪些方面改进函数模型?
预设答案:一是改进所选函数类型,二是改进函数中的参数。具体改进方法最好是结合函数图像的直观,结合数学运算,不断进行调整。如果利用计算机辅助改进效果最佳。
【设计意图】
通过计算和图像比对看误差与偏差,验证函数模型的优劣,让学生体会到建立函数模型过程只有更好,没有最好。改进函数模型也往往需要将直观与计算结合起来,因为仅凭感觉调整一个系数可能会影响原本拟合较好的数据。
五、课堂小结
1. 你认为怎样选择函数拟合数据误差更小?
2. 数学建模的主要步骤有哪些?如何撰写数学建模论文?
六、布置作业
农业专家在研究某地区玉米在不同生长阶段的植株高度时,得到了以下数据:
|
生长阶段 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
植株高度/cm |
0.67 |
1.75 |
3.69 |
7.73 |
16.55 |
32.55 |
53.38 |
97.46 |
153.6 |
174.9 |
180.79 |
请建立适当的函数模型刻画该地区玉米的生长规律,并将研究过程写成一篇论文。
(参考函数模型:指数函数模型f1(x)=aebx,逻辑斯谛模型f2(x)=k/1+ce-rx,分段函数模型等。)
本网站旨在促进我国基础教育的信息交流,促进基础教育事业的发展。本网站转载的资料,如果作者不希望我们在网上使用其作品,请立即与我们联系,我们会在收到您的意见后立即从网上移除有关内容。未经人教网的明确书面许可,任何人不得复制或对人教网所属的服务器做镜像。

