3.1.3 函数的奇偶性（第3课时）
教学课时：第3课时
教学目标：
1.结合具体函数，了解函数奇偶性在研究函数图象时的作用；
2.能研究一个具体函数的性质，并作相应图象；
3.能结合函数的奇偶性，研究函数的对称性，提升数学抽象、数学运算和逻辑推理等核心素养。
教学重点：
研究函数的性质，做出函数的图象。
教学难点：
形成研究函数性质的一般方法。
教学过程：
一、情境与问题
问题1：研究一个函数的性质，你觉得研究什么内容？
预设答案：定义域、值域、单调性、奇偶性、图象
问题2：你认为了解了函数的哪一个性质，就可以说了解了这个函数？
预设答案：知道了函数的图象，就可以说基本了解了这个函数。
二、实践操作
例1. 研究函数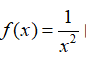
的性质，并作出相应的图象。
第一步：教师引导学生给出定义域，判断并证明
是定义域上的偶函数
第二步：引导学生证明函数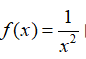
在（0，+∞）上是减函数。
第三步：作出函数的图象。
问题3：函数f(x)的图象关于y轴对称，可以表示为f(-x)=f(x)，如果函数f(x)的图象关于直线x=2对称，又可以怎样表示？
预设答案：f(2-x)=f(2+x)，
自然语言表达：函数f(x)的自变量的两个值对应的点关于点（2，0）对称（或者以（2，0）为中点）时，对应的函数值相等。
三、逻辑提高
例2：请指出二次函数f(x)=x2+4x+6的图象的对称性，并证明.
【设计意图】对称性的结论初中就知道，但是初中得到的结论是直观感知的，会运用数学符号语言给出证明，提高了逻辑推理核心素养.
问题4：已知二次函数f(x)=x2+4x+6，试判断f(x-2)的奇偶性，并由此能否给出一般结论？
预设答案：f(x-2)是偶函数，理解f(-x-2)=f(x-2)
四、课堂练习
1.课本第109页练习B第1题
2.课本第111页练习B第7题
五、课堂小结
1. 研究函数性质的一般方法步骤；
2. 函数对称性的数学表达。
六、布置作业
课本第110页习题3-1C第3题
本网站旨在促进我国基础教育的信息交流，促进基础教育事业的发展。本网站转载的资料，如果作者不希望我们在网上使用其作品，请立即与我们联系，我们会在收到您的意见后立即从网上移除有关内容。未经人教网的明确书面许可，任何人不得复制或对人教网所属的服务器做镜像。
