教学课时：1课时

　　教学目标：

　　1.使学生能在实际问题中找到不等关系，并能列出不等式和不等式组，抽象成数学问题；

　　2.引导学生运用对比联想，得到不等式的简单性质，并学会用综合法证明不等式；

　　3.使学生掌握“作差法”比较两个数或两个代数式的大小；

　　4.让学生对不等式性质进行直观解释和逻辑证明，逐步提升学生的代数推理能力，发展直观想象和逻辑推理素养.

　　教学重点：

　　引导学生运用对比联想，得到不等式的简单性质，并学会用综合法证明不等式；掌握做差法比较两个数或两个代数式的大小.

　　教学难点：

　　不等式性质的直观解释和逻辑证明.

　　教学过程：

　　一、复习回顾：

　　【学生活动1】

　　1.自己阅读课本P58 —情境与问题；

　　2.再举出两个描述不等关系的实例；

　　3.回忆前面学习过哪些不等号，思考书P58想一想.

　　【设计意图】

　　通过实际问题引入，选取贴近学生实际生活的素材，通过高速公路上车速的限定范围创设情境，并且让学生通过模仿，类比写出客车和货车行驶速率满足的不等式.使学生能在实际问题中找到不等关系，并能列出不等式和不等式组，抽象成数学问题.

　　根据学生的实际认知水平回顾不等式的概念，并可以补充更多相关的实例，激发学生的学习兴趣.

　　【学生活动2】

　　4.怎样理解两个实数之间的大小；

　　5.对比等式，不等式会有哪些类似性质；

　　6.与同伴进行交流讨论

　　【设计意图】

　　将实际的不等关系写成对应的不等式时，需要用到相应的数学符号，为后面学习不等式性质做铺垫；借助数轴，让学生观察实数的大小与数轴上点的运动的关系，体会数轴上点的运动引起实数大小的变化规律，进而直观感受到比较大小的变化规律，进而直观感受到比较较大小的原则，这有助于学生从形的角度思考问题，体现数形结合的数学思想方法.

　　二、讲授新课：

　　（一）不等式的性质及证明　　

　　对于任意两个实数a，b,如果a>b，那么a-b是正数；如果a<b,那么a-b是负数；如果a=b，那么a-b等于0.它们的逆命题也正确.　　

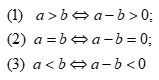
　　这是比较实数大小的三个基本事实，需要向学生强调的是：其中的符号表示的是充要条件.另外在教学时，要向学生渗透化归与转化的数学思想方法，并强调结论中的a,b也可以是代数式. 也就是说，要比较两个代数式的大小，只要比较它们的差与0的相对大小即可.

　　【设计意图】

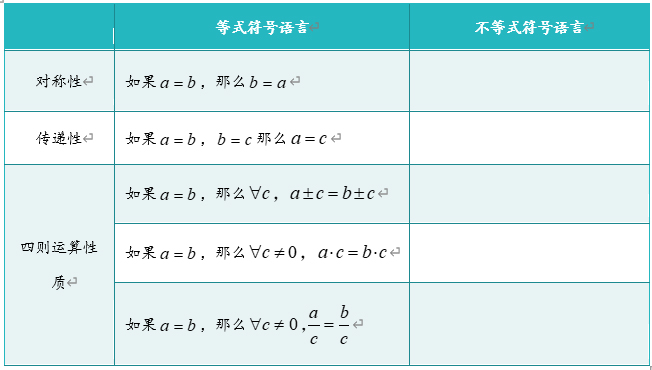
　　1.学生在前面已经学过等式的性质，初中时也学习过不等式的一些性质，可以通过等式性质复习，引导学生对比联想不等式的性质.

　　2.带领学生对性质进行证明，掌握“作差法”、“综合法”.

　　3.复习“配方法”.

　　【学生活动3】

　　7. 回答书中P60 — “尝试与发现”中的问题；

　　8. 与同伴进行讨论.

　　【设计意图】

　　引导学生深入辨析不等式的性质，同时用逻辑用语描述相应的性质，目的是发展学生的数学抽象和逻辑推理素养.

　　（二）不等式性质的推论与证明　　

　　例2 求证：

　　【设计意图】

　　1.练习刚讲解过的“作差法”、“不等式的基本性质”；

　　2. 得到不等式性质的推论1~4，引导学生从运算（加、减、乘、除、乘方）的角度，类比等式性质提出一些命题，然后判断其真假，并对真命题给出证明，从而培养学生的问题意识，积累发现问题、提出问题的经验，进一步发展逻辑推理素养.

　　推论5的证明留待下一节课去解决.

　　三、归纳总结：

　　1.不等式的性质和推论

　　2.作差法　　

　　3.综合法