一、引言

　　我们在文^［1］中阐明了总体分布和总体分布特征的内涵，并以频率稳定于概率的原理和古典概型知识为基础，介绍了用样本频率直方图估计总体直方图的原理。本文将在文［1］的基础上，进一步考虑一类特殊变量的总体分布估计问题，该类变量能够依据问题背景完全确定其值域，且值域中仅包含有限个值，可以用更加简单直观的方式表达它所对应的总体分布。针对这类特殊变量，我们将借助案例引进总体密度、总体密度图和总体饼图等知识，以及用样本估计总体分布密度的方法与原理。

　　一般而言，如果学生了解大数定律和蒙特卡罗方法，那么我们就能以此为基础，从总体均值估计问题出发，介绍放回简单随机抽样、简单随机抽样、分层抽样和样本均值估计总体均值的原理（详见^［2］第3章第2节）。但高中生并不具备这样的基础，因此需要另辟蹊径。

　　二、有限离散变量及其密度

　　案例1考察某地区高中生的视力情况。

　　首先要思考的问题是：用怎样的变量描述“某地区高中生的视力”，以及如何通过此变量描述“高中生的视力情况”？为方便讨论，我们先用数学语言定义总体和近视变量。

　　假设这个地区高中生总数为N，用ωi表示第i位高中生，则总体可以表达为

　　Ω=｛ω1，ω2，…，ωN｝。

　　定义近视变量x在第i位学生的值这样，

　　“考察某地区高中生的视力情况”就等价于考察近视变量的变化规律，即考察该变量的总体分布。显然，近视变量x的值域为

　　D=｛0，1｝。（2）

　　由（2）式可知：变量x不可能在区间（0，1）上取值，因此它在区间（0，1）上取值的比例为0；在区间［-1，0.5）上的比例是视力正常学生的比例；在区间［1，5）上的比例为近视学生的比例；在区间［0，2）上的比例为1。

　　一般地，对于任何一个区间，若0和1都不在这个区间中，那么变量x在该区间上的比例就为0；若0在这个区间中，而1不在这个区间中，变量x在该区间上的比例就为视力正常学生的比例；若1在这个区间中，而0不在这个区间中，变量x在该区间上的比例就为近视学生的比例；若0和1都在这个区间中，变量x在该区间上的比例就为1。这样，要想知道变量x在任何区间上的比例，只要看该区间包含0或1的情况。因为0，1的特殊意义，我们把0，1分别看成为一个区间，记作［0，0］，［1，1］。

　　设近视学生的比例为p，那么，近视变量在区间组（-∞，0），［0，0］，（0，1），［1，1］和（1，∞）上的比例分别为0，1-p，0，p和0，我们可以用图1直观表达总体分布的这种特征。

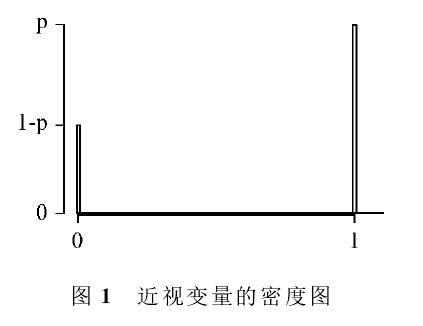
　　图1由坐标横轴上的垂直线段构成，高度为1-p的线段表示变量在区间［0，0］上的比例为1-p，高度为p的线段表示变量在区间［1，1］上的比例为p。为交流方便，称图1为近视变量的密度图。近视变量的密度图直观表达了该变量在区间组（-∞，0），［0，0］，（0，1），［1，1］和（1，∞）上的比例变化情况，它完全决定了近视变量的分布。

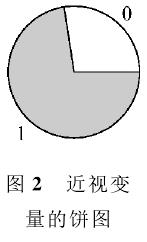
　　还可以用饼图直观表达近视变量的这一总体分布特征，如图2所示。其中，白色扇形的面积与圆的面积之比为1-p，阴影部分扇形的面积与圆的面积之比为p。我们称图2为近视变量的饼图。和密度图类似，饼图通过圆中各个扇形的面积的差别直观表达了该变量在区间组（-∞，0），［0，0］，（0，1），［1，1］和（1，∞）上的比例变化情况，它完全决定了近视变量的分布。因为（-∞，0），（0，1）和（1，∞）上的比例为0，图中不显示比例为0的部分。

　　一般地，如果总体的某个变量的值域仅有有限个不同的“值”，并且这些“值”可以由问题背景所确定，就称此变量为有限离散变量。由案例1问题背景知近视变量的值域为｛0，1｝，它是有限离散变量。

　　例12010年我国大陆居民的年龄变量和性别变量都是有限离散变量吗？

　　解注意到2010年我国大陆居民总数为正整数，易知年龄变量的值域中仅有有限个不同的值。但是由于该值域中的值不能由问题的背景确定（即不能在普查之前预知），所以年龄变量不是有限离散变量。

　　依据常识，我们知道居民性别变量的取值为“男”或“女”，即性别变量的值域可以由问题的背景所确定，所以性别变量为有限离散变量。

　　综上所述，年龄变量不是有限离散变量，性别变量是有限离散变量。

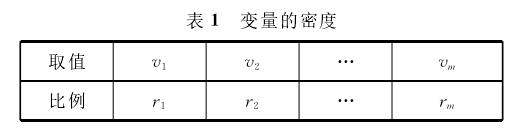
　　为表述方便，用v1，v2，…，vm表示有限离散变量值域中的所有不同值（m为值域中的不同值的个数）；对于任意1≤i≤m，用ri表示变量在单点区间［vi，vi］上的比例。类似于案例1，这些单点区间上的比例完全决定了总体分布，称之为该变量的分布密度，或总体密度，或密度。

　　三、离散变量的密度表示和估计方法

　　通常，可以用表格的形式表达总体密度，如表1所示：表格的第一行为有限离散变量的值，第二行为相应于各个值的比例。

　　例2求案例1中近视变量的值域，并用表格的形式表达近视变量的密度。

　　解由案例1中的变量表达式（1）知：近视变量只可能取0和1两个值，所以该变量的值域为｛0，1｝。进一步，近视变量在［0，0］和［1，1］上的比例分别为1-p和p，所以其密度表为表2。

　　对于有限离散变量，都可以依据其密度绘制像图1一样的图形，并称这样的图形为该变量的分布密度图，或总体密度图，或密度图；还可以依据其密度绘制像图2一样的图形，并称这样的图形为该变量的分布饼图，或总体饼图，或饼图。

　　在案例1中，近视变量的分布完全由其密度所决定，密度表、密度图和饼图是密度的不同表达方式，密度表给出了变量取值与相应比例的对应关系，密度图和饼图直观展示了各个比例变化的几何直观。

　　在实际应用中，我们并不知道离散变量取各个值的比例，因此无法制作其密度表，也无法绘制其密度图或饼图。初中阶段介绍了用样本数据的频率条形图估计总体的统计方法，现在我们可以进一步解释这种方法的内涵。

　　案例1续近视变量的分布密度、密度图和饼图的估计原理。

　　为估计近视变量的分布密度，仅需估计该变量的密度表中的各个比例。下面用放回简单随机抽样的原理解决近视变量的分布密度的估计问题。

　　沿用前面案例1中的符号，则近视变量在区间［0，0］上的高中生全体（即全体视力正常的高中生）可以表示为

　　A1=｛ωx（ω）=0，ω∈Ω｝；

　　在区间［1，1］上的高中生全体（即全体近视高中生）可以表示为

　　A2=｛ωx（ω）=1，ω∈Ω｝。

　　这样，我们就把问题转换为A1和A2中的学生数与学生总数之比例各是多少？从初中学过的古典概率知识角度，可以将A1和A2中的学生比例分别看成是事件A1和A2的古典概率，依据频率近似于概率的思想，可以用其频率估计概率。

　　因此，可以用放回简单随机抽样依次获取样本观测数据x1，x2，…，xn（其中n为样本容量），其实施过程可以看成是进行了n次重复试验，第i次的实验结果为xi。对于第一个样本观测数据x1，如果它等于0，就意味着在第一次抽到的学生视力正常，这等价于第一次实验的结果是事件A1发生；否则意味着第一次抽到的学生的视力不正常（近视），这等价于第一次的实验结果是事件A2发生。其它数据的含义可以同样解释。

　　在图1的绘制过程中，分别用f（A1）和f（A2）替代近视变量在［0，0］和［1，1］上的比例，用垂直条形代替垂直线段，可以得到近视变量样本观测数据的频率条形图，如图3所示。依据前面的分析，图3中的各个条的高度会随着样本容量的增加分别稳定于图1中各个线段的高度，因此可以用图3估计图1。

　　在图2的绘制过程中，分别用f（A1）和f（A2）替代近视变量在［0，0］和［1，1］上的比例，可以得近视变量样本观测数据的饼图，如图4所示。类似地，依据频率稳定于概率的原理，可以用图4估计图2。

　　类似于案例1续，对于任何有限离散变量，都可以用放回简单随机样本观测数据的频率条形图（饼图）估计相应的总体密度图（饼图）。依据频率稳定于概率的思想，样本观测数据的频率条形图（饼图）会随着样本容量的增加而稳定于总体密度图（饼图）。

　　四、不同抽样方法对于总体密度估计效果的比较

　　由文［1］知简单随机抽样避免了放回简单随机抽样可能得到的“坏样本”，因此简单随机样本观测数据的频率条形图（饼图）对于总体密度图（饼图）的估计效果更好，下面通过一个随机模拟的例子说明这一点。在随机模拟中，用到了R软件程序代码，该软件是一个自由、免费、源代码开放的统计软件，可以在［2］的前两章附录中找到R软件的基本使用方法。

　　例3考察的总体为某高中班级的40名学生，变量为近视变量x。表3依学号次序列出了总体中各学生的变量取值。

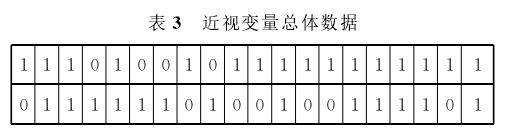
　　试比较容量为20的放回简单随机样本和简单随机样本数据的频率条形图估计总体变量条形图的效果。

　　解首先利用如下程序代码绘制总体分布条形图。

　　

　　总体变量条形图如图5所示，其中视力正常学生的比例为0.275，患近视学生的比例为0.725。

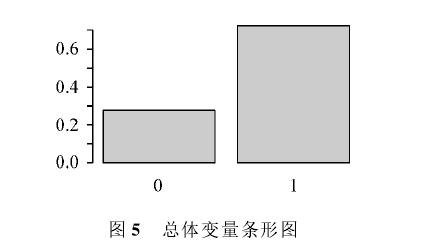
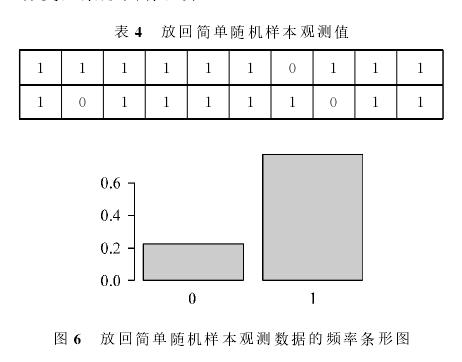
　　利用如下的程序代码模拟容量为20的放回简单随机样本观测数据，并绘制相应的频率条形图。抽出的样本数据如表4所示，相应的频率条形图如图6所示。

　　reSampleX<-sample（totalX，20，replace=T）

　　myF<-as。factor（reSampleX）

　　myT<-table（myF）

　　myTotalP<-prop。table（myT）

　　barplot（myTotalP）

　　与图5比较可以发现：样本数据频率条形图与总体变量条形图有差异。

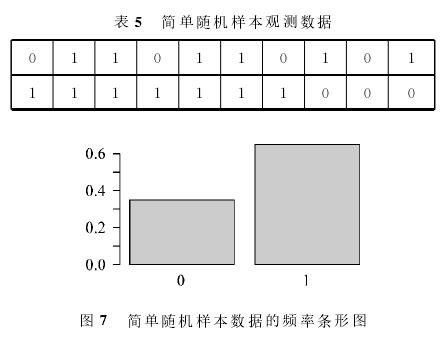
　　利用如下的程序代码模拟容量为20的简单随机样本观测数据，并绘制相应的频率条形图。抽出的样本数据如表5所示，相应的频率条形图如图7所示。

　　sampleX<-sample（totalX，20）

　　myF<-as。factor（sampleX）

　　myT<-table（myF）

　　myTotalP<-prop。table（myT）

　　barplot（myTotalP）

　　与图5和图6相比可以发现：虽然简单随机样本观测数据的频率条形图与总体变量条形图之间存在差异，但是与放回简单随机样本观测数据的频率条形图相比，这种差异小多了。

　　由于抽样的随机性，两次抽取样本数据的频率条形图一般会不同，因而比较的结论也会有所不同。但是对大量重复抽样结果进行比较，可以发现简单随机样本效果好的次数更多，即简单随机样本的效果好于放回简单随机样本。类似地，如果能有效利用额外信息，那么比例分层抽样对于总体密度（条形图，饼图）的估计效果好于简单随机样本的效果。五、总结

　　对于有限离散变量，总体分布密度能决定总体分布，还可以用总体密度图或总体饼图表示总体分布；可以用放回简单随机样本、简单随机样本和比例分层随机样本的观测数据的频率条形图（饼图）估计总体密度图（饼图），并且简单随机抽样估计效果好于放回简单随机抽样估计，在有效利用额外信息的前提下，分层随机抽样估计效果好于简单随机抽样估计。

　　参考文献

　　［1］李勇，章建跃，张淑梅。样本估计总体的内涵与教学探究———直方图与抽样［J］。数学通报，2016，55（11）

　　［2］李勇，金蛟。统计学导论-基于R语言［M］。北京：北京大学出版社，2016