一、问题的提出

　　对于有限总体，人们常用随机抽样的方法获取样本数据，并用样本估计总体。问题是如何向学生介绍常用抽样方法（如简单随机抽样和分层抽样）和样本估计总体的概率统计学原理，使学生了解这些抽样方法的来龙去脉？我们认为，这是统计课程教材建设中的关键问题之一，对学生的统计学创新能力和统计学素养的提升有积极意义。

　　现行高中数学教材大都按如下框架介绍抽样方法和样本估计总体知识：

　　1、关于抽样知识，仅介绍抽样方法的实施步骤，强调其好处，阐明应用情境；

　　2、关于用样本估计总体，仅强调样本均值可以估计总体均值，直方图和条形图可以描述总体分布特征；等等。

　　这样的教材框架操作性强，可以使学生明白“怎么做”，但其缺点也很明显：

　　1、直接告诉结果，容易导致注入式教学；

　　2、抽样方法和样本估计总体的内容分离，不能展示这些统计学知识的来龙去脉；

　　3、易使学生将统计学误解为简单的加、减、乘和除的计算公式；

　　4、不利于培养学生们统计学创新能力。

　　那么，该如何改进抽样方法和样本估计总体的传统框架呢？如何介绍它们的概率统计学原理呢？我们认为，这一问题的解决，有赖于如下基础性工作：理清样本估计总体的内涵，明确抽样的目的，然后在此目标下用初中的概率统计知识解释随机抽样和样本估计总体的原理。

　　在术语“样本估计总体”中，“估计总体”是指估计总体变量的取值规律。那么什么是总体变量的取值规律呢？在我们所见参考文献中，都是以随机变量的分布观点来解释总体变量取值规律，超出了初中毕业生的知识范围。因为高中课标要求教材先安排统计再安排概率，因此我们不能用这种观点来解释总体变量取值规律。

　　进一步的研究发现：对于有限总体，变量不具备随机性，因此不能以随机变量分布的观点解释总体变量的取值规律。事实上，个体是研究对象的最小单元，总体由所有的个体构成，因此总体和个体的概念与随机现象没有任何关系；个体的任何一种特征指标都可以称为变量，即变量的载体是个体，变量是总体到特征指标值域的一个映射，因此变量也不具备任何随机性。不失一般性，这个值域可以看成是实数的一个子集，比如性别变量的值域是｛男，女｝，我们可以用1表示男，0表示女，这样｛0，1｝也可以作为性别变量的值域。那么应该如何解释总体变量取值规律的内涵呢？什么是样本估计总体的内涵？下面我们试图以4个案例探讨这一问题的解答。在案例的探究过程中，我们将逐步引入一些新术语，以阐释总体变量取值规律的内涵，介绍放回简单随机抽样、简单随机抽样、分层抽样和总体分布特征的估计原理。

　　二、关于总体、总体变量及其分布案

　　例1人口普查问题。

　　准确掌握全国的人口数据，可以为科学制定国家的许多方针、政策及发展战略提供依据。2010年我国进行了第六次人口普查，调查中国居民人口和住户的基本情况，内容包括：姓名、性别、年龄、民族、受教育程度等。这里居民为调查对象，而每位居民都有各自的性别、年龄、民族、受教育程度等量化特征。人口普查就是对全国人口逐户逐人地进行的一次性调查登记。

　　类似于人口普查这样的收集数据的方法，称之为普查。在普查中，类似于居民这样的调查对象称为个体，所有的个体构成总体，类似于性别、年龄、受教育程度这样的个体量化特征称为总体变量，简称为变量。

　　案例1续考察我国大陆居民年龄，普查者想要了解该变量在各个年龄段的居民比例，这是国家制定教育、医疗、保险等政策的基础。如在《2010年第六次全国人口普查主要数据公报（第1号）》中公布了一些年龄段的居民比例数据（如表1所示）。

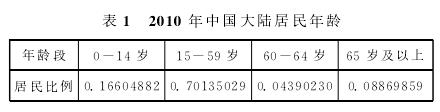
　　通常，人们把各年龄段居民占总居民数的比例的全体称为年龄变量的分布，简称为年龄分布。在进行这次全国普查之前，中国居民的人口和住户的基本情况为未知现象，该现象由诸如性别、年龄、民族、受教育程度等变量所刻画。

　　一般地，对于定义在总体上的变量，人们关心变量值位于指定区间中的那些个体数目的比例，称之为此变量在该区间上的比例，并且称此比例的全体为总体变量分布，简称为总体分布或分布。

　　在统计学研究中，人们用总体变量刻画未知现象，并通过分析变量的分布状况来认识未知现象的变化规律。

　　三、总体分布的表示

　　案例22010年我国居民年龄结构状况分析。

　　2010年我国居民的年龄分布包含了总体中所有年龄信息，即各个年龄段的居民比例信息。在实际应用中，我们经常要了解一些特定年龄段的居民比例数据，并常常把这些数据用表1的方式表示出来。

　　我们还可以用图1直观表示这些年龄段的平均比例数据。其中，区间［0，15）上的矩形面积等于15岁以下（不包括15岁）居民比例，区间［15，60）上的矩形的面积等于15岁至60岁（包括15岁，不包括60岁）居民比例，区间［60，65）上的矩形面积等于60岁至65岁（包括60岁，不包括65岁）居民比例，区间［65，M］（包括65岁和最高年龄M）上的矩形面积等于65岁以上居民比例。

　　图1是从平均角度看这三个年龄段中的居民分布情况：在区间［0，15）中，平均每岁（每单位年龄中）居民人数为0。011069922；在区间［15，60）中，平均每岁（每单位年龄中）居民的比例为0。015585562；在区间［60，65）中，平均每岁居民的比例为0。008780459；在区间［65，M］中，平均每岁居民的比例为0。001612702。因此，年龄在区间［0，15）中的居民平均比例处于低水平，年龄在区间［15，60）中的居民平均比例处于高水平。由此可以预计：随着时间的推移，中国大陆居民的老年人平均数将会增加，年青人平均数将会减少。因此，必须采取相应的国策以应对人口老龄化和后继无人的问题。

　　可以看到，年龄变量有如下特征：（1）取值为实数，（2）值域不能事先预知。通常，我们用图1这样的图形表示这类变量的分布特征。为交流方便，称这样的图形为总体变量比例直方图，或总体直方图，或简单称为直方图。

　　总体直方图是总体分布的一种刻画，不同的区间分组，对应着不同的总体直方图，它们共同决定了总体分布。在实际应用中，通常是像案例2一样，通过具体的区间分组所对应的总体直方图，探讨区间组内的各个区间上平均比例的变化特点，并将这些变化特点都称为总体分布特征，或简称为分布特征。

　　要注意，总体分布和总体分布特征是两个不同概念，任何一个总体分布特征都由总体分布所确定，反之通常不对。

　　四、样本、样本容量和抽样方法

　　显然，通过普查获取所有个体变量的取值之后，就可以计算所关心区间的个体比例，绘制总体直方图，进而分析总体分布特征。但在实际应用中，由于种种原因不允许普查，由部分个体的变量值估计总体分布特征就成为人们研究的课题。

　　（1）样本、样本容量

　　全国人口普查会耗费国家大量的人力、物力和财力资源，不能随意进行。我国从1949年至今分别在1953年、1964年、1982年、1990年、2000年与2010年进行过六次全国性人口普查。国家统计局在1982年人口普查的基础上，自1982年开始，每年进行一次全国人口抽样调查，形成了一项调查制度

　　一般地，要估计总体分布特征，需要从总体中抽出部分个体，并设法用这些个体变量值的分布特征来估计总体分布特征。为交流方便，我们称从总体中抽出的那些个体的变量值组成一个样本，组成样本的那些个体（即抽出的那部分个体）的数目称为样本容量。

　　（2）放回简单随机抽样、样本数据和样本频率直方图

　　下面以图1所示的年龄分布特征的估计为情景，展示一种抽样方法和用样本分布特征估计总体分布特征的概率统计学原理。

　　案例32010年我国大陆居民的年龄特征的一种估计方法。

　　为讨论方便，引入几个数学符号。用N表示大陆居民总数，用ωi表示第i位居民，则总体可以表达为

　　Ω=｛ω1，ω2，…，ωN｝。

　　为分别估计年龄在区间［0，15）、［15，60）、［60，65）和［65，M］中居民人数的比例，用x（ω）表示居民ω的年龄，则年龄在区间［0，15）中的所有居民可以表示为

　　A1=｛ω0≤x（ω）<15，ω∈Ω｝；

　　年龄在区间［15，60）中的所有居民可以表示为

　　A2=｛ω15≤x（ω）<60，ω∈Ω｝；

　　年龄在区间［60，65）中的所有居民可以表示为

　　A3=｛ω60≤x（ω）<65，ω∈Ω｝；

　　年龄在区间［65，M］中的所有居民可以表示为

　　A3=｛ω65≤x（ω）≤M，ω∈Ω｝。

　　这样，我们就把问题转换为A1，A2，A3和A4中的居民数与居民总数之比例各是多少？从初中学过的古典概率知识角度，可以将A1中居民比例看成是事件A1的古典概率，依据频率近似于概率的思想，可以用其频率估计概率。类似地，A2，A3和A4中的居民比例都可以看成是各自的古典概率，都可以用各自的频率来估计。可以按如下的步骤获得所关心事件的频率：

　　就像案例2一样，也可以用图形表示这些频率所蕴含的总体分布特征。如图2所示，其中的四个矩形的面积依次等于事件A1、事件A2、事件A3和事件A4发生的频率。

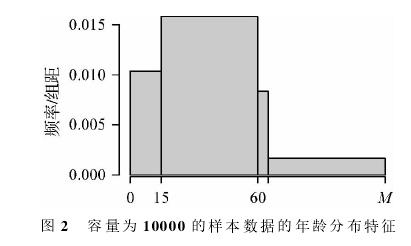
　　图2是用一个容量为10000的样本观测数据所绘制的图形，已经看不出它与图1中的总体直方图有何差别，其原因是样本容量已经很大了。图3是用容量为100的样本观测数据所绘制的图形，它与总体直方图有明显的差别，其原因是样本容量较小。

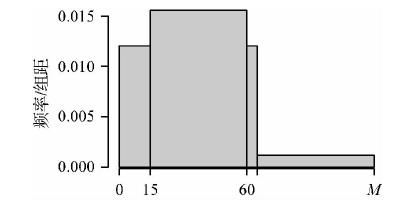
　　为交流方便，我们将图2和图3都称为年龄样本频率直方图。

　　上述方法建立的年龄样本频率直方图具有随机性：即使在相同的样本容量之下，两个样本所对应的年龄样本频率直方图会有所不同。依据频率近似于概率的思想，年龄样本直方图会随着样本容量的增加而稳定于相应的总体直方图，即可以通过样本频率直方图认识总体分布特征。

　　一般地，用取后放回的方法从总体中依次任意取出n个个体，就可以将这些个体所对应的变量值X1，X2，…，Xn作为样本，称之为放回简单随机样本，并称这样的抽样方法为放回简单随机抽样。为交流方便，人们称像案例3中年龄样本频率直方图这样的图形为样本频率直方图，简称为频率直方图。

　　显然，在案例3中，放回简单随机抽样的结果是不能事先确定的，因此样本X1，X2，…，Xn具有随机性；当实施放回简单随机抽样后，我们得到了n位居民的年龄样本观测数据x1，x2，…，xn，这些数据是确定的实数，不再具有随机性。实际上，年龄样本观测数据是年龄样本的观测结果，有了这些观测结果才能完成频率直方图的绘制工作。

　　为交流方便，我们将实际完成抽样过程之后所得的所有个体变量数据称为样本观测数据。为区分样本和样本观测数据，我们用大写英文字母X1，X2，…，Xn（或H1，H2，…，Hn，或Y1，Y2，…，Yn，等等）表示样本，用小写的英文字母x1，x2，…，xn（或h1，h2，…，hn，或y1，y2，…，yn，等等）表示样本观测数据。在实际应用中所谈及的数据，通常指的是样本观测数据（随机样本的观测结果）。虽然样本观测数据已经固化，不再具有随机性，但是这些数据中的每一个数都是来自总体的随机观测结果，它们包含总体分布信息。

　　在探讨总体分布特征的估计问题过程中，案例3的依据是古典概型和频率稳定于概率的思想。由此引入放回简单随机抽样方法，以及用放回简单随机样本的频率直方图估计总体直方图的方法，并可以得到结论：随着样本容量的增加，频率直方图稳定于总体直方图。

　　（3）简单随机抽样

　　案例3续在案例3中，我们是用放回简单随机抽样的方法获取样本的观测数据x1，x2，…，xn，然后用样本频率直方图估计总体分布特征。直觉告诉我们，在放回简单随机抽样中，可能会重复抽到同一个个体，甚至会出现取出的居民都是同一人的情况，此时样本的观测数据为x，x，…，x，其中x为该居民的年龄。对于图1中的分割区间组，此样本观测数据所对应的频率直方图的可能情况如图4所示。

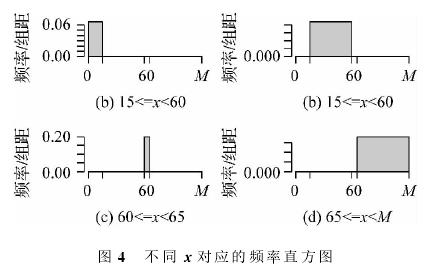
　　图4中有4个频率直方图，分别对应于该居民的年龄位于区间［0，15）、［15，60）、［60，65）以及［60，M］的情况。显然，这些频率直方图都与图1中的总体年龄分布直方图有很大差异，因此来自同一居民的年龄样本观测数据对于总体分布特征的估计效果极差，即这样的样本观测数据为“坏”样本观测数据，简称为坏样本。

　　如何避免放回简单随机抽样所产生的这种坏样本呢？一个简单的方法就是将抽样过程修改为：用取后不放回的方法从总体中依次任意取出n个个体，然后将这些个体所对应的变量值X1，X2，…，Xn作为样本。

　　一般地，用取后不放回的方法从总体中依次任意取出n个个体，然后把这些个体所对应的变量值X1，X2，…，Xn作为样本，称之为简单随机样本，并称这样的抽样方法为简单随机抽样。

　　统计学家已经证明，简单随机抽样优于放回简单随机抽样。因此，在实际应用中总在这两种方法中选用简单随机抽样。这里介绍放回简单随机抽样，是为了描述简单随机抽样的来龙去脉，使具有初中知识背景的高中学生感受从古典概型和频率稳定于概率到放回简单随机抽样，以及从放回简单随机抽样到简单随机抽样的知识发展过程，从而使他们得到统计学思维模式的熏陶，更有效地提升他们的统计学素养。

　　（4）分层抽样

　　下面的案例将进一步展示从简单随机抽样到分层抽样的知识发展过程。案例4已知某高中学校有360名男生，440名女生，关心该高中学校中学生的身高分布特征。为估计学生身高分布特征，如何利用已知信息抽取容量为40的学生身高样本？

　　分析：现在的总体由该高中学校的所有学生构成，有两个定义在此总体上的变量，即身高和性别，并且已经知道哪些学生为男生，哪些学生为女生，要估计的是身高变量特征。需要解决的问题是应该如何获取样本才能使得样本频率直方图有更好的估计效果。

　　当然可以采用简单随机抽样获取样本观测数据，然后用样本频率直方图估计总体分布特征。但高中男生的身高会普遍高于女生，即男生身高分布与女生身高分布之间存在很大差异。而用简单随机抽样有可能得到全是男生（或全是女生）的样本观测数据，此时样本频率直方图会呈现男生（或女生）的身高分布特征，这种特征与总体身高分布特征有差异，结果导致估计的效果变差。

　　我们能否利用已知的学生性别变量信息，改进抽样方法，以有效地避免这种全是男生（或女生）的“坏样本”，从而提高估计精度呢？

　　答案是肯定的，具体做法如下：将总体分割成两个子总体Ω1和Ω2，其中Ω1是由全体男生构成的，Ω2是由全体女生构成的。在Ω1中用简单随机抽样选取18名学生，在Ω2中用简单随机抽样方法选取22名学生，测量所有选出学生的身高值，得到容量为40的样本观测数据h1，h2，…，h40。

　　一般地，在抽样时，可将总体分成互不交叉的层（要求各层的变量的分布特征互异），然后按照一定的比例，从各层中用简单随机抽样获取一定容量的样本，将各层取出的个体合在一起作为最终抽取的样本。这种抽样方法称为分层抽样。（stratifiedsampling）。

　　在分层抽样中，如果能像案例4中一样，使每一层所抽出的个体数都与该层所包含的个体数成比例，就称这种分层抽样为比例分层抽样。

　　五、总结

　　本文通过案例1阐释总体变量取值规律的内涵，从中抽象出总体分布的概念；通过案例2展示了总体分布特征的表达方法，引入总体直方图的概念；案例3则是以初中的概率统计知识为起点，以总体分布特征的估计为导向，阐明了放回简单随机抽样和样本频率直方图估计总体分布特征的原理；案例3续中，在分析放回简单随机抽样弊端的基础上引入简单随机抽样方法，由此说明了简单随机抽样的优点；案例4则是在分析简单随机抽样缺点的基础上，阐明了有效利用额外信息的分层抽样方法。这些案例都是从问题情景出发，经过数学抽象，再利用已有概率统计知识分析和解决问题，并在此过程中引出新概念、新知识。

　　此外，这些案例包含处理抽样问题的数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析的过程，每一案例都体现了特定的统计学思维方式，对培养学生的统计创新意识，提升学生的统计学素养都有积极的意义。

　　希望本文能起到抛砖引玉的作用，乐见统计学教育同行能够给出更完美的案例，以促进我国统计学教育的蓬勃发展。